Задача №33.
Два однородных цилиндра веса 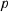 каждый положены на внутреннюю поверхность полого цилиндра, как указано на чертеже (рис. 6). Они поддерживают третий цилиндр веса
каждый положены на внутреннюю поверхность полого цилиндра, как указано на чертеже (рис. 6). Они поддерживают третий цилиндр веса 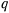 . Определить зависимость между указанными на чертеже углами
. Определить зависимость между указанными на чертеже углами 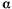 и
и 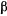 , если
, если 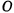 — центр большого полого цилиндра,
— центр большого полого цилиндра, 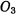 — центр третьего цилиндра и
— центр третьего цилиндра и 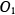 и
и 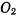 — соответственно центры первого и второго цилиндров, на которых покоится третий.
— соответственно центры первого и второго цилиндров, на которых покоится третий.
Решение:
Положение равновесия, симметричное относительно вертикали, которая проходит через центр полого цилиндра, определяется всего одним параметром. Заметим, что если выбрать систему осей 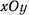 с началом в центре полого цилиндра, направив
с началом в центре полого цилиндра, направив
ось  вертикально вверх, то координата
вертикально вверх, то координата  центра тяжести всей системы определяется равенством
центра тяжести всей системы определяется равенством
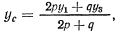
где 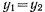 — соответственно координаты центров тяжести нижних цилиндров,
— соответственно координаты центров тяжести нижних цилиндров, 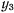 — координата центра тяжести верхнего цилиндра. В силу симметрии:
— координата центра тяжести верхнего цилиндра. В силу симметрии:

где 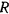 — радиус полого цилиндра,
— радиус полого цилиндра,  — радиус нижних цилиндров,
— радиус нижних цилиндров, 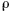 — радиус верхнего цилиндра. Тогда для ус получим
— радиус верхнего цилиндра. Тогда для ус получим

Приравнивая нулю приращение 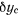 , получаем условие равновесия системы:
, получаем условие равновесия системы:
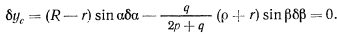
Нетрудно установить постоянную зависимость между параметрами 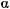 и
и 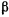 системы:
системы:
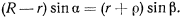
Эта зависимость сохраняется при всех возможных перемещениях системы. Дифференцируя последнее равенство, будем иметь
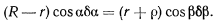
Исключая из уравнений (1) и (2) величину 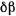 получим для положения равновесия
получим для положения равновесия
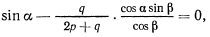
откуда
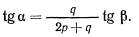
Таким же образом методы аналитической статики применяются и для решения задач о равновесии пространственных систем.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:

