Задача №42.
Два одинаковых стержня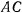 
и 
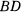, весом 
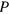и длины а каждый, могут свободно вращаться на шарнирах 
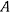и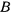 
. Они соединены шарнирам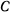и 
и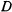 
с третьим стержнем, расположенным горизонтально и имеющим вес Q и длину а<>- Вся система находится в равновесии в вертикальной плоскости. Определить реакции шарниров А и С, если угол а известен (рис. 45).
Решение:
Система находится в равновесии. Чтобы определить реакции в точке 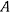, освободим эту точку и введем вместо имеющейся связи неизвестную пока по величине и по направлению силу реакции 
. Обозначим горизонтальную проекцию этой силы через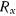 
, а вертикальную — через 
. Освобожденная система получает новые возможные перемещения, при которых точка 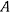может уже перемещаться как по горизонтали, так и по вертикали. Сообщим сначала горизонтальное перемещение точке 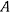. Обозначим это перемещение через 
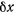. Точки 1, 2, 3 приложения сил тяжести так же совершат некоторые перемещения. Подсчитывая работу всех сил на перемещении системы, будем иметь
Выражая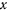 
и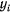 
через угол 
, получим
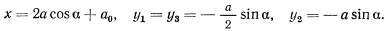
Теперь уравнение работ примет вид
Отсюда уже легко определить
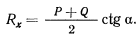
Среди возможных перемещений освобожденной системы находится поворот стержня 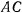вокруг точки 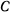. Как известно, обобщенная сила, соответствующая перемещению поворота, равна сумме моментов сил, действующих на твердое тело, относительно центра вращения. Подсчитывая эту обобщенную силу и приравнивая ее нулю, будем иметь
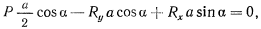
откуда после подстановки значения 
сразу же получим
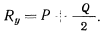
Для определения реакции в точке 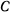освободим еще стержень 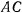в точке 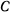, заменив существующие связи силами реакции 
, 
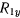. Освобожденный от связен стержень 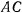может перемещаться поступательно как в горизонтальном, так и в вертикальном направлениях. Подсчитывая работу на этих перемещениях, легко найдем
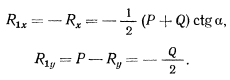
Аналогично решается задача и в том случае, когда на систему наложены неидеальные связи — например связи, определяемые трением. При решении задач необходимо освободиться от таких связей, введя неизвестные силы реакции, удовлетворяющие принимаемому закону трения. В большинстве встречающихся задач таким законом является закон Кулона, в соответствии с которым сила трения определяется как сила, пропорциональная давлению,- производимому точкой тела на связь. Эта сила препятствует свободному движению материальной точки и уравновешивает активные силы, действующие па точку. При этом коэффициент пропорциональности не является постоянной величиной. Он зависит от характера движения, от характера действующих активных сил и обычно определяется неравенством
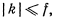
где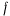 
— коэффициент трения, соответствующий началу движения материальной точки.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
