Оглавление:
Другие приёмы и методы
Наряду с рассмотренными выше методами при решении уравнений в целых числах используются и другие приёмы. Например, в следующем примере учитывается тот факт, что уравнение является однородным.
Пример №71.
Решить в целых числах уравнение 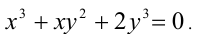
Решение:
Заметим, что если у = 0, то x = 0, и, значит, пара (0;0) удовлетворяет уравнению. Пусть 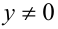 , тогда поделим обе части уравнения на
, тогда поделим обе части уравнения на 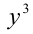 :
:
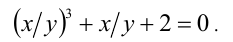
Обозначим t = х/у, тогда имеем кубическое уравнение 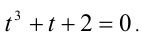 Подбором находим корень t= — 1. Делением многочлена
Подбором находим корень t= — 1. Делением многочлена 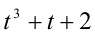 на
на 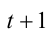 получаем:
получаем:
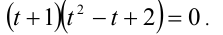
Убеждаемся в том, что данное кубическое уравнение имеет единственный корень t = — 1, что соответствует у = -x . Положим x = р , где р — произвольное целое число, не равное 0. Тогда у = -р, и имеем бесконечно много решений в виде пар чисел 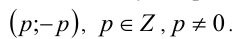 Объединяя все полученные решения, приходим к ответу.
Объединяя все полученные решения, приходим к ответу.
Ответ: 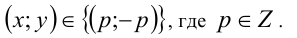
Иногда при решении уравнения или неравенства в целых числах не требуется привлечения каких-либо специальных методов решения: достаточно внимательно проанализировать его ОДЗ.
Пример №72.
Найти все целые числа x, удовлетворяющие неравенству 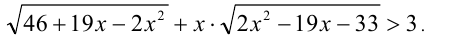
Решение:
ОДЗ: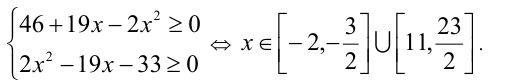
Очевидно, что только два целых числа x = -2 и x = 11 содержаться в ОДЗ. Проверка показывает, что лишь второе удовлетворяет неравенству.
Отметим, что количество различных приёмов и способов, используемых при решении задач на натуральную и целочисленную арифметику, слишком велико, и для ознакомления и, более того, успешного усвоения этих приёмов необходимо решение достаточно большого числа разнообразных задач.
Многие из упомянутых приёмов решения и типов конкурсных задач рассматриваются в книге. Рекомендуем желающим более углублённо изучить данный раздел обратиться к этому изданию.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

