Другие геометрические образы, которые могут быть использованы в механике. Краткий обзор

Другие геометрические образы, которые могут быть использованы в механике. Краткий обзор

• Метод представления векторных величин, которого мы до сих пор придерживались исключительно, явно не является единственно возможным методом. Вы также можете связать другие геометрические элементы с другими механическими elements. So например, система силы, приложенной к твердому телу, может быть согласована с шариковым винтом. Движущийся вектор, который рассматривается как комбинация 2 х точек, полученных в определенном порядке, можно понимать как первое звено в ряду величин, которые образуются путем присоединения не только точек, но и других простейших элементов пространства, в определенном порядке. E. Study занимался систематическим изучением таких геометрических величин.

Он ввел следующую сумму. D. крест, образованный комбинацией из 2 прямых линий.1 находится на конечном расстоянии, а другой 1 на пересечении первой вертикальной плоскости, и, следовательно, бесконечно. 2.Бипланы, взятые в определенной последовательности, представляют собой систему из 2 х плоскостей, не перпендикулярных друг другу. 3.Стиль поворота ToyNpeS , образованный точками и плоскостями. 4.Некоторые прямые системы называются двигательными и импульсными. 5.Например, скользящий сферический вектор Эти понятия используются не везде, поэтому они ограничиваются перечислениями. Потому что до сих пор эти понятия не нашли важного применения в mechanics.

В разделе упражнений будет показано, что систему векторов можно всегда привести к таким двум векторам, из которых Ъдин лежит на произвольной прямой, не параллельной главному вектору. Людмила Фирмаль

Для их геометрического исследования hepsus Lorde de dollars Французская версия работы исследования, или статья Люсьена Леви Bissel Bauuu. Упражнение 1.Некоторый вектор сходимости Pb Pb …Указывает, что модуль K результирующего вектора Pn определяется выражением Число = B 2 cos Здесь первая сумма распределяется по всем векторам, а вторая сумма распределяется по всем векторным комбинациям. 2.In для того чтобы система векторов была равна нулю, необходимо и достаточно устранить главный момент на 1 произвольной точке, которая не находится на 3 прямых. 3.Взаимность векторной теории.

Возьмем воображаемую сферу x2 y2 g24 + 1 = 0 центральная точка O, на прямой, сопряженной с P1 относительно вектора P сфера, используя проективные X1, Y2, x и момент M1, проективный x = A4P Xx = Направление B M, 1, перпендикулярно плоскости ORX. It указывает, что существует взаимность между вектором Px и Pp, то есть что Px находится на прямой, сопряженной с P1, и его проекция равна моменту вектора P1.То есть Xx = Dp Y1 = L4p 2 = преобразование Клейна, если оно специфично, указано Кенигсом. 4.Согласно предыдущему преобразованию, система векторов 5 соответствует одной системе. Указывает, что главный момент 1 й системы относительно точки о равен основному вектору 2 й системы. 

5. Если одна из предыдущих систем 5 или 5 сводится к паре, то другая сводится к вектору, проходящему через точку O, и наоборот. 6.Найдите пространственную кривую, момент которой равен нулю, а касательная прямой линии. Когда центральной осью системы является ось z, дифференциальные уравнения для этих кривых принимают вид: мкг = х гг ых Где параметр потока. Показано, что наиболее общая кривая, удовлетворяющая этому уравнению, определяется уравнением. 

Где p произвольная функция от 0. 7.Указывает, что контактная поверхность некоторых кривых в предыдущей задаче сфокусирована на точке контакта. 8.In бесчисленными способами можно сформировать систему из 2 векторов, P и, которые эквивалентны системе данного вектора и ортогональны друг другу. Указывает, что строки P и Phi образуют комплексное число 2 го порядка. Мы идем к одному и тому же комплексу и ищем комплексы, которые образуются главным моментом на всех точках пространства. 9. Если 2 вектора P и равны данной системе, то их общие перпендикуляры обычно пересекают центральную ось этой системы. 

10. Вам будет дано несколько пар и полученная пара. Указывает, что проекционная площадь параллелограмма, построенного на плоскости по вектору результирующей пары, равна алгебраической сумме проекционной площади параллелограмма, построенного по вектору компонентных пар. 11. П, П….. P M , и соответственно m , с вектором, образующим систему, эквивалентную нулю… Другой момент Ось P , P ,…Система векторов, относящихся к соотношению P 5, доказывает П l4 П Л1 + … + Р Л4 к = 0 Вектор относительно P , P ,…Сначала P должен доказать теорему об одном векторе P системы 5, используя, что главный момент P равен нулю. 

Координаты центра тяжести Мебиуса. Пусть L1L2L3D4 тетраэдр. Центроидными координатами точки M являются алгебраические значения 4 параллельных векторов Px, P3, P4, которые необходимо соединить с вершинами Lx, A A и A4 так, чтобы центры этих параллельных векторов совпадали с точками M. значение Pb P 8 P определяется с точностью до общего множителя. Линейные однородные уравнения относительно L. PbPz P определяет плоскость, где расстояние от 4 вершин пропорционально коэффициентам Px, P P и P .Если эти коэффициенты равны, то плоскость будет бесконечной.

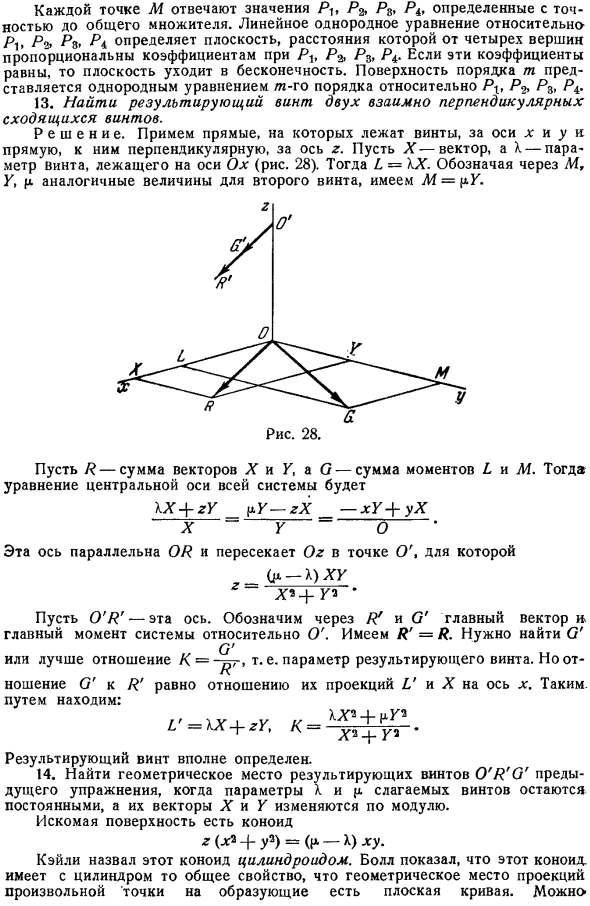
• Поверхность порядка m представляется однородным уравнением порядка n относительно P , P P. 13. Найдите полученный винт из 2 взаимно перпендикулярных сходящихся винтов. Решение. для осей x и y возьмем прямую линию, на которой расположены винты, а для оси z прямую, перпендикулярную им. Пусть X вектор, а X параметр винта на оси Ox рис.28.Тогда = X. Если вы укажете аналогичную величину для 2 го винта В И, У, л аналог, это будет M = P Y. Если P сумма векторов X и Y, а O сумма моментов b и M, то уравнение для центральной оси всей системы выглядит следующим образом: Х4 ый Р. Г gX ху + ух Х П О г Эта ось параллельна OP и пересекает Og в точке O. А Х ху Х + Г Сделать о ПРОМАЛЬП своей оси.

P и O обозначают главный вектор и главный момент системы относительно O. Существует P = R. вам нужно найти O. Или лучше, соотношение K = og, т. е. результирующий винт parameters. No. К Присоединение O к P равно отношению проекций D и X на оси X. Таким образом, вы можете увидеть следующее: Г=ХХ+гГ, К= Полученный винт четко определен. 14.Если параметром является лира, найдите траекторию движения винта O r o Screw в результате предыдущего упражнения. Винтовые члены остаются постоянными, а их векторы X и Y изменяются по модулю. Желаемой поверхностью является Коноид + г = стр.

Существует бесчисленное множество способов приведения заданной системы векторов к двум векторам. Людмила Фирмаль

Кейли назвала этот Коноид цилиндрической формой. Шар показал, что этот Коноид имеет общее с цилиндром свойство, что геометрическое положение проекции любой точки на генератор является плоскостью curve. In кроме того, мы можем доказать, что эта кривая является конусом цилиндра. 15. В общем случае доказано, что результирующий винт из 2 произвольных винтов фиксированного положения представляет собой цилиндр, когда параметры этих винтов остаются постоянными и вектор изменяется. В оси Og возьмите общую вертикальную линию для обоих винтов. 

Из всех нецилиндрических управляемых поверхностей единственной поверхностью, где геометрическое положение проекции любой точки на генератор является плоской кривой, является цилиндр. См. Аррен, Vieppe 1aZosg gyopsy taidie, 1900 12 месяц, Nnsagd, Дитто, 1901 1 месяц, OetoiNp, то же самое. 17.Любая система движущихся векторов всегда равна 6 векторам, направленным вдоль 6 ребер тетраэдра. 18. Пусть 8 ABC тетраэдр. Пусть направление 5L, 8B, 8C, оставить в качестве положительного направления на edge. In кроме того, на каждом ребре основания, таком как AB, оно выражается в направлении AB, 6, C, X, p, как положительное направление вращения вокруг противоположного края 5C.

Инвариант BX MU 4 указывает, что N2 имеет значение И ВС8АСА8В АВ8СГ Где V объем этого тетраэдра. 19.To сделать систему скользящего вектора равной нулю, необходимо и достаточно, чтобы 6 составляющих 6, , C, X, p и y были равны нулю. 20.To сделать систему движущихся векторов равной нулю, необходимо и достаточно, чтобы сумма моментов для каждого из 6 ребер тетраэдра была равна нулю. 21. Система скользящих векторов в 1 плоскости соответствует 1 вектору, 1 паре или нулю. 22. Система векторов скольжения в 1 плоскости соответствует 3 векторам, направленным вдоль сторон произвольно взятого треугольника в этой плоскости. 

Чтобы векторная производная вектора всегда была перпендикулярна вектору, необходимо и достаточно, чтобы длина этого вектора была постоянной. 24.In чтобы векторная производная вектора всегда была ориентирована вдоль него, необходимо и достаточно, чтобы этот вектор имел определенное направление. 25. Смешанное произведение 3 векторов сближения ВСУ АП АР АП3 и прогноз Ху уу ху ху х Г и х2, х3, У3, Х3 это скаляр X2 U1 Y Я не уверен. 2 3 Объем, размер и знак параллелепипеда, построенного на этих векторах, равны. Показать его 1.Смешанный продукт изменяет знак, как только 2 фактора перестраиваются. 2. Смешанное произведение трех полюсных векторов является скаляром 2 го рода раздел 34. 3.

Смешанное произведение 3 х осевых векторов является 1 м видом скаляра. 4. Смешанное произведение 3 векторов является скалярным произведением 1 скалярного произведения вектора и 2 других векторных произведений. 26.Центральная плоскость. Представлена система связанных векторов. Кг…

Применяется в точке Ip a .Когда точка P движется параллельно основному вектору K, положение этой точки Po существует, что указывает на то, что результирующий вириар, равный сумме вириаров всех векторов для Po, исчезает. Геометрическое положение точки Po представляет собой плоскость, перпендикулярную P. Это центральная плоскость. 27.Центр.

Смотрите также:

Предмет теоретическая механика

Векторные производные	Кинематика точки. Определения
Характер симметрии вектора	Движение точки