Дробно-рациональная функция

Дробно-рациональная функция

Дробно-рациональной функцией (или рациональной дробью) называется функция, равная отношению двух многочленов, т. е. , где — многочлен степени 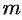, a — многочлен степени .

Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя, т. е. ; в противном случае
(если ) рациональная дробь называется неправильной.

Всякую неправильную рациональную дробь можно, путем деления числителя на знаменатель, представить в виде суммы многочлена и правильной рациональной дроби , т.е.

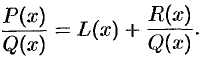
Например, — неправильная рациональная дробь. Разделим числитель на знаменатель в столбик:

Получим частное и остаток . Следовательно, .

Правильные рациональные дроби вида

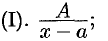
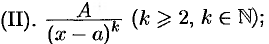
(корни знаменателя комплексные, т. е. );

(, корни знаменателя комплексные), где — действительные числа, называются простейшими рациональными дробями I, II, III и IV типов.

Теорема 31.8. Всякую правильную рациональную дробь , знаменатель которой разложен на множители

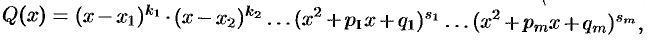
можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:

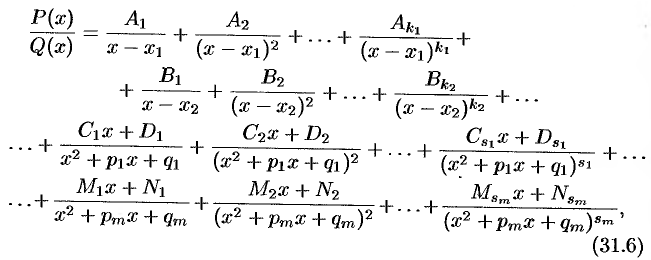
где — некоторые действительные коэффициенты.

Поясним формулировку теоремы на следующих примерах:

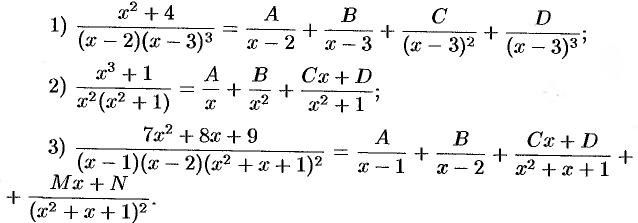
Для нахождения неопределенных коэффициентов в равенстве (31.6) можно применить метод сравнивания коэффициентов. Суть метода такова:

1. В правой части равенства (31.6) приведем к общему знаменателю ; в результате получим тождество , где — многочлен с неопределенными коэффициентами.

2. Так как в полученном тождестве знаменатели равны, то тождественно равны и числители, т. е.

3. Приравнивая коэффициенты при одинаковых степенях (по теореме 31.5 о тождестве многочленов) в обеих частях тождества (31.7), получим систему линейных уравнений, из которой и определим искомые коэффициенты

Пример №31.3.

Представить дробь в виде суммы простейших дробей.

Решение:

Согласно теореме 31.8 имеем:

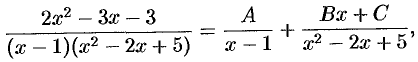
т. е.

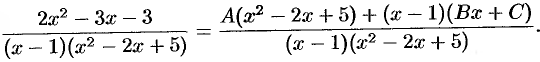
Отсюда следует

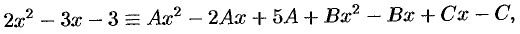
т. е.

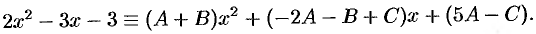
Приравнивая коэффициенты при , получаем

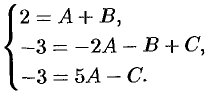
Решая систему, находим, что . Следовательно,

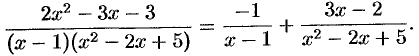
Для нахождения неопределенных коэффициентов применяют также метод отдельных значений аргумента: после получения тождества (31.7) аргументу придают конкретные значения столько раз, сколько неопределенных коэффициентов (обычно полагают вместо значения действительных корней многочлена ).

Дополнительный пример №31.4.

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

• Решение задач по высшей математике

Другие темы по высшей математике возможно вам они будут полезны:

Метод интегрирования по частям

Понятия о рациональных функциях

Интегрирование рациональных дробей

Универсальная тригонометрическая подстановка