Оглавление:
Дробно-линейное программирование
В дробно-линейном программировании (ДЛП) целевая функция является дробно-линейной вида
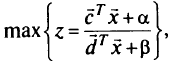
где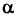 
и 
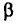— скалярные константы; 
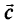и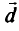 
— векторы, сформированные из исходных данных; 
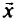— вектор искомых переменных:
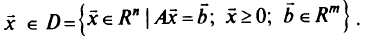
Таким образом, в качестве целевой функции используется отношение двух линейных функций; условия ограничения задачи остаются линейными: линейные равенства и неравенства.
Обычно предполагают, что знаменатель целевой функции положителен и не обращается в нуль в области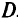 
.
Задачи ДЛП применяются в тех приложениях, когда оптимизируются относительные показатели. Особенно часто такие задачи встречаются в финансовой области: планирование деятельности корпораций, управление статьями банковского баланса и т.п.
Поверхности уровня целевой функции в задаче ДЛП линейны, поскольку, если взять значение целевой функции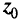 
, то
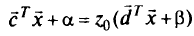
или
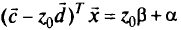
линейное уравнение, если знаменатель целевой функции в области 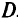не равен нулю.
Таким образом, если задача ДЛ П имеет оптимальное решение, то по крайней мере одна крайняя точка из области 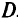будет оптимальной. Однако линии уровня целевой функции расходятся как лучи от множества вращения размерности 
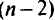. Множество вращения — это множество всех точек пересечения нулевой линии уровня числителя
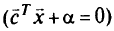
с нулевой линией уровня знаменателя
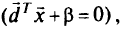
т.е. множество точек, удовлетворяющих системе уравнений
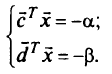
Вращая линию уровня целевой функции в направления вектора 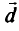против часовой стрелки, увеличиваем значение целевой функции; вращая линию уровня по часовой стрелке — уменьшаем значение целевой функции.
Если знаменатель целевой функции отрицателен на , то дробь следует умножить на (-1), не изменяя при этом условия максимума или минимума целевой функции.
Для решения задач ДЛП применяют преобразование переменных и процедуру обновления целевой функции.
Преобразование переменных. Путем преобразования переменных задачу ДЛП при положительном в области знаменателе сводят к задаче линейного программирования. Делается замена
переменных
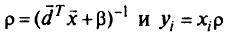
для всех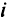 
.
Задача ДЛП принимает вид:
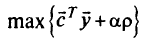
при ограничениях
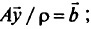
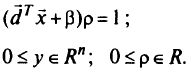
В результате появляется новая переменная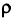 
, и имеем задачу линейного программирования: найти
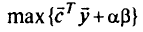
при ограничениях
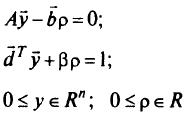
Эта задача имеет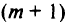 
ограничение и 
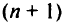переменную.
Пример:
Решить задачу ДЛП:
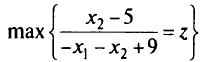
при ограничениях
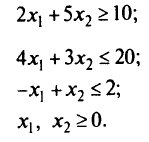
После замены переменных получим задачу линейного программирования:
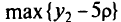
при ограничениях
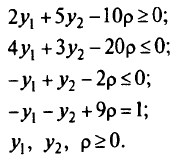
Решая ее симплекс-методом, находим
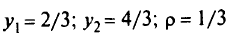
или оптимальное решение
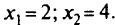
Обновление целевой функции. Задача ДЛ П решается как последовательность задач линейного программирования, где на каждой итерации пересчитывается градиент целевой функции
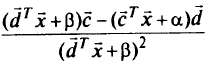
в полученной оптимальной точке. С новым значением градиента решается новая задачалинейного программирования. Процесс повторяется до тех пор, пока решение не будет изменяться.
При обращении в области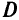 
знаменателя в нуль могут быть следующие случаи:
- Знаменатель принимает как положительные, так и отрицательные значения — в таких случаях целевая функция
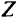нe имеет ни конечного максимума, ни конечного минимума. - Знаменатель всюду равен нулю — всем точкам из области 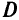соответствуют неопределенные значения .
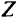- Векторы
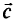и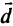 
коллинеарны.
3.1. Множество вращения пусто, тогда нулевые линии уровня числителя и знаменателя параллельны, но не совпадают друг с другом; 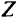нe ограничено сверху и не определено в крайней точке.
3.2. Множество вращения не пусто — числитель и знаменатель имеют идентичные нулевые линии уровня; 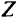постоянно в области 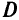, кроме некоторых точек, где оно имеет значение 0/0.
- Векторы 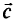и 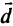не коллинеарны.
4.1. 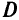— подмножество множества вращения — всем точкам из области 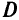соответствуют значения 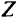вида 0/0.
4.2. Знаменатель всюду равен нулю — 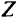= 0 всюду, кроме тех точек из 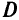, принадлежащих множеству вращения, где оно принимает значение 0/0.
4.3. В области 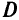существуют точки, где знаменатель не равен нулю — здесь могут быть:
- конечные минимумы и конечные максимумы;
- конечные минимумы, но неограниченные максимумы;
- неограниченные минимумы и максимумы.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
