Доверительные оценки для н и о2, когда один из параметров известен

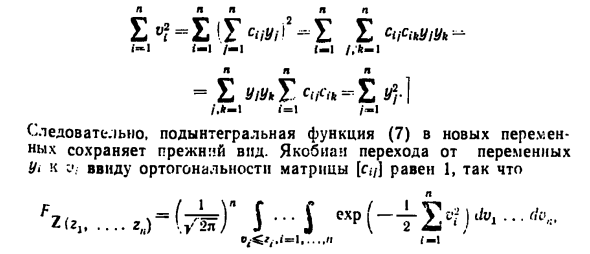
Доверительные оценки для н и о2, когда один из параметров известен

• Рассмотрим выборку Х-, (= 1, …, это, из нормального распредэ распредел Хщ, о2) со средним ц и дисперсией о2. оценочные показатели и дисперсия x —-. ± Vх „So2 = -LU (X, -x) * = IVxl-x \ П ± ми II • * »фут ** 1 = 1 1 = 1 1 = 1 Предположим, что один из параметров (.i пли а2 извес- гтен. TM-Y — ц) / а) имеет нормальную информацию V /, 1) (см. § 7, п. 3) и а-дов рптельный интервал для получения &> (jfo / 2 <К «(X —ц) / а <Х | а.2) = -а, или ГХ- <кв / а / 1 ^ Г) = а. где .v, -а-квантиль распределение Л ‘@, 1). .А / @, 1) имеем х „= -Х \ -а, следовательно, а-доверительнын интер- интервал можно представить в виде X — a.V | a / 2 / l / «/ T <<< X + oxi-a’-ilVn. Ш Jopustim, что | j, известно, требуется оценить о2. точечного оценивания а2 естественно вместо выборочной дисперсии взять статистику который отличается от S \ заменой выборочного среднего на тео- теоретическое. величина п ‘~ Ъ-ИJ.B) имеющуюся долю% 2п (см- § 7, п. 4). а-довернтельнын интервал для о2 в виде (X, — цJ, я = я т = я где л *, »-а-кваптнль маршрут х2» — 2. Несмещенная оценка дисперсии.

В случае независимого выбора распределение выборочное среднее является несмещенной оценочной теоретической теоретического среднего 59 Однако выборочная дисперсия имеет смещение MS5- М (-L? X? -L-? Х, Х,) = MXf- 1-1 (, / = 1 L MX? -? Nli (MX, J = f 1-—) 20o наблюдаются обычно вместо S20 замечают несмещенную оценку ? _ S6 = -L- V (X, -X) *. 1 ° ni ^ jv 3. Доверительные интервалы для и и о2, когда оба параметра неизвестны. Допустим, что оба параметра \. И о2 выделены л ‘(| л, о2) неизвестные. Б), Б) образуем следующие: п Vri () C-n) lS, -l? (Xt-X) «. C) ? -1

Введем нормированные ел. У, = (Х, -ц) / о, / — = 1 п, которые независимы и N @, 1) -распределены. то значение C) можно переписать в виде Людмила Фирмаль

Таким образом, распределение вероятностных значений C) не за- разрешать неизвестные параметры и а2, доверительные интервалы Лемма 1. Пусть ,,, »= 1, …, л, независимы, N @, ^ -распре- ^ -распределены, С = [сц, я, / = 1, …. п] -ортогональная пхп-матрица: 2г ,, с, ч = 0 при \ фк, у д—, 1. Положим _ ijYj, iv = \ Я. E) 60 Это время ел. В. Зит я = л, …. п, являются независимыми. Л / (О, 1) -рас- 1) -распределенными. В /, t = l п, равна (-1 , Овместная ф. Р. Ел. В. Z, -, t = 1, …. л, F_ .. = (Z, <21, i = l ZB1? …. 2Л) л 4Yi <2t ‘/ = 1 л) равняться степени плотности G) по области л Произведенный в этом интеграле заменен переимленными по формелам л f (= 5) ty0 /, i = \ п. (8)

Так как матрица о ортогональной, то из (8) вытекает R-I / -I [Ортогональное преобразование постоянной длины векторов: Л ЯП ЯП Следовательно, подынтегральная функция G) в новых явлениях я могу найти данные о прежнем виде. У> кВ; вытекает из (8), (9). Выберем в условиях леммы 1 ортогональную лХл-матрицу С = [сп] так, чтобы с „, = 1 / Уп, /» = 1, …, п. Значения сц при хФп нам не важны, только матрица была бы ортогональной (напри- (например, 1егко проверить, что годятся с, — / в форме / <«) • Тогда 1 = 1 1 = 1 (= 1 E (У.- Yf- ^ t Yf-nV- т ф? 1 = 1 1 = 1 1 = 1 1 = 1 Учитывая C), D) и определение% 2 „и / ,, _ i (см. § 7), приходим к следующему утверждению.

• Лемма 2. Пусть X:, i = l, …, «, независимы и N (\ i, а2) -распре- а2) -распределены. — »» 1 = 1 1 = 1 независимы и распределены соответственно N @, 1) и% 2п- \, а отношения- отношение имеет распределение tn- \ Щ. Ы леммы 2 получают а-доверительный интервал для о2: <(n-D & lx *;., (X, -; _ i), (Ю) где .va (Xn-i) — «- квантиль Х ^ граспределения, и-доверительный интервал для ц: Х-х ^ а о (<„,) S / 1 / n <ц <X —хв., 4 (/„ _,) S / Vn, (И) где x, (/ n-i) -a-квантиль / л-грасмределення.

Если в A0) или А1) оставить только одно неравенство, то получим односторонние н / 2-доверительные границы, верхние или нижние. Людмила Фирмаль

Смотрите также:

Предмет статистики

Экспоненциальное распределение	Сравнение дисперсии в двух выборках
Распределение х2 с п степенями свободы	Примеры линейных моделей