Оглавление:
Теорема. Пусть функция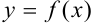 
непрерывна и дифференцируема в некоторой окрестности точки 
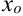. Тогда:
- если производная
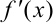при переходе через точку 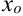меняет знак с плюса на минус, то точка 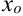является точкой максимума; - если производная 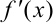при переходе через точку 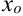меняет знак с минуса на плюс, то точка 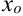является точкой минимума.
Представим критерий нахождения точек экстремума функции в виде схемы:
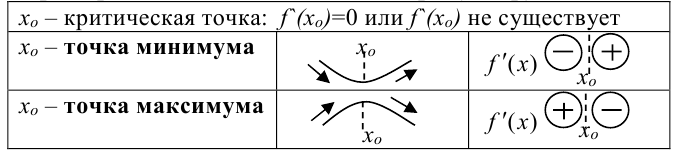
Для нахождения промежутков монотонности и экстремумов функции будем использовать следующий алгоритм:
- Найти область определения функции.
- Найти первую производную функции.
- Определить критические точки первого рода (
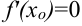или 
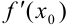не существует). - На числовой оси отметить критические точки и определить знаки производной на каждом из получившихся интервалов.
- Найти интервалы монотонности, выписать точки экстремума функции (если они есть), используя соответствующие критерии, вычислить значения функции в точках экстремума.
Пример №14.1.
Найдите промежутки монотонности и экстремумы функции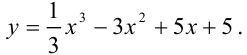 
Решение:
1. Данная функция определена на множестве 
.
2. Найдем первую производную функции: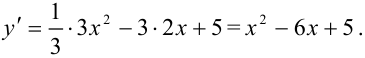 
3. Определим критические точки первого рода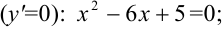 
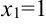или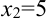 
.
4. На числовой оси отметим критические точк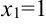и и 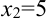. Эти точки разбивают область определения функции на три интервала 
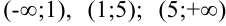. Расставим знаки производной функции 
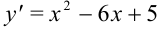на каждом из полученных интервалов:
при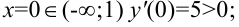 
при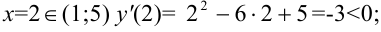 
при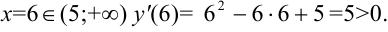 
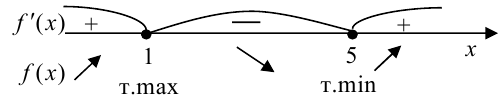
5. Согласно критерию возрастания и убывания функция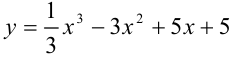 
возрастает при 
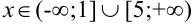, убывает при 
.
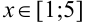Согласно критерию нахождения точек экстремума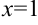 
— точка максимума, 
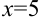— точка минимума. Для нахождения экстремумов вычислим значения функции в этих точках:
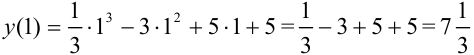— максимум функции;
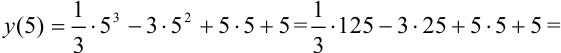
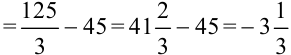— минимум функции.
Ответ: 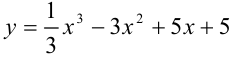возрастает при 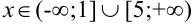, убывает при ;
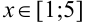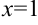— точка максимума; 
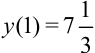— максимум функции;
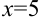— точка минимума; 
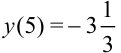— минимум функции.
Пример №14.2.
Найдите промежутки монотонности и экстремумы функции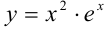 
.
Решение:
1. Данная функция определена на множестве .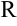
2. Найдем первую производную функции по правилу производной произведения:
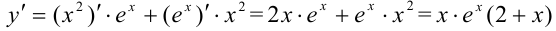
3. Определим критические точки первого рода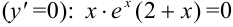 
; 
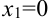или 
(
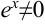для всех 
из множества ).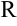
4. На числовой оси отметим критические точк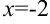и 
и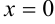 
. Эти точки разбивают область определения функции на три интервала 
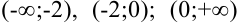. Расставим знаки производной функции 
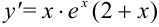на каждом из полученных интервалов:
5. Согласно критерию возрастания и убывания функция 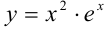возрастает при 
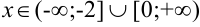, убывает при 
.
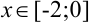Согласно критерию нахождения точек экстремума 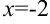— точка максимума, 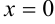— точка минимума. Для нахождения экстремумов вычислим значения функции в этих точках:
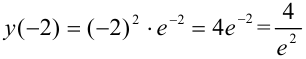— максимум функции;
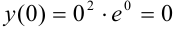— минимум функции.
Ответ: 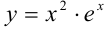возрастает при 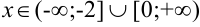, убывает при ;
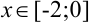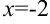— точка максимума; 
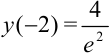— максимум функции;
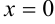— точка минимума; 
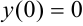— минимум функции.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие точек экстремума и экстремумов функции |
| Необходимые условия существования экстремума |
| Понятие выпуклой и вогнутой функции |
| Критерий выпуклости-вогнутости функции и точек перегиба. |
