Оглавление:

















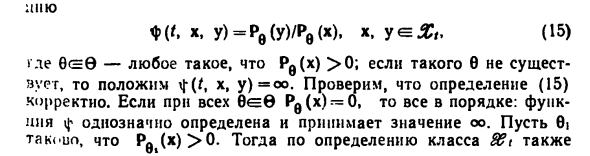







Достаточные статистики в дискретной модели
- В статистической мо- модели (#?, 38, {Р}), можно рассчитывать на уточнение наших св сведении об истинном распределении вероятностей Р? получаю в результате эксперимента с распре- информация о своем распределе- распределенной вероятностен. интерес представляет только та информация задавать различающиеся элементы Р из {Р}. статистические выводы нескольких статнстнках-функициях от о. чтобы не потерять информацию по интересующему нас вопросу?
Нас интересует такой, по возможности мини- минимальный, набор статистик G * | (х), …, Г * (х)) = Т (х), который является содержательная информация Такая статистика Т (х) будет проведена называться достаточной статистикой для нашей модели. 2. Примеры. (I) Пусть a? = {X ,, = (.v, ™): а / = 0 или 1, i = l, …. и}, Р „(х„) = 8 $ «A -8)» — \ sn = Xl + … + xn, 0де О <0 <1. Это хорошо известная схема испытаний Бернулли. используется статистика sn {Q = sn / n.
Например, рассмотренные в статистика несу г информация только о таких чертах {Р} и, следовательно, ничего не дать для решения задач различаем элементы Р. Людмила Фирмаль
Допустим, статистика sn приняла не- некоторое значение s. именно из резюме если мы наблюдали случай s ,, = s, то естественно перейти к модели с выбором пространством S? j = (x ,,: *! + … + xn = s) и семейством условных вероятност- вероятностных мер, получаемых из Ре сужением на 96%. как видно, не требуется от 6, единственного элемента-равномерного распределения на 26%. дополнительная вероятностная информация помимо той, что х „еЯ? 4-, никак не связана с параметром 6, и потому статистическая информация параметрре 6.
Соображения, лежащие в основе приведенных рассуждений, Реализуем испытания Бер- Все, что вам нужно-это столы или урны. случайный чисел) 0 <0 <1, и урну с N шарами я + 1 цветов, учитывая долю шаров 1-го цвета равны биномиальной вероятности р, = С „’0’A — 0) n ~’, i = = 0, 1, …. п (в качестве N можно взять наименьшее число, при где все NPl, я = 0, я, …. п, целые). возьмем еще л + 1 ури, причем уриа с номером i, t = 0, I, …, п, содер- содержит Сп ‘(Сп ° = 1) шаров, занумерованных „„’ наборами (х \, … ¦ ¦-, хи), х / = 0- или 1, / = 1, …, п, представляющих ровною единицу. Организуем теперь двухступенчатый выбор. + 1 цветов и отмечается цвет i вы можете найти ваш номер. извлекается шар и номер извлеченного шара-последовательность (х \, …. х „) -объявляется результатом полного эксперимента.
- Элементарный вероятностный расчет показывает, что результат опыта — (* i, …, х „) -представляет собой реализацию испытуемых- испытании Бернулли с вероятностью 6 выпадения 1. С другой стороны, поскольку вторая ступень нашего сложного опыта связана с па- параметром 6 только через ‘номер i-результат первого этапа, совершенно ясно, что к информации о 6 первой ступени опыта, второй ступень ничего нового добавить ие может. (II) Пусть Я? = {Х „- = (; с, xR): xi-0, 1, 2 t = 1, 2, … …. »}, а мера Ре соответствует независимой выборке из пуассо- мовского распределения с параметром 0> О: 7 121
Оценочный параметр G-теоретического среднего выбора жит выборочное среднее x-sjn, «„ —d] xt. ную модель в предположении s ,, = s с выбором пространством 8t? S = (x: xi + … + X ,, = s) и условной мерой Pe (xn | a? S) = Pe (xn) / pe (a? S), х „ея? *. B) Пнаменатель в Б) представляет собой вероятность того, что сум- сумма независимых пуассоновских ел. в., с параметром 6 каждая, имеется Легко проверить, что при сложении двух незави- независимых ел. в., распределенных по Пуассону с параметрами>. соответственно, получая ел. в. X + Y также имеет распределе- выделение Пуассона с параметром А, + ц: г »0 -Е- * — * -tr * = -У —- г! (u-v) l и !? Jv \ (u- 0 0 о)!
Отметить, что С) представляет собой частный случай так называемого полиномиального распределе- распределе(при и = 2-биномиального с вероятностью 1/2). следует, что искусственный выборку объема я из пуассоповского можно построить, моделируя сна- сначала пуассоповскую ел. значение s, то моделируется опыт по случайному размещению s результат последнего опыта записываем в виде набора (х \, хз, …, х „), где лг, -число шаров, попавших в Я вижу, что этот результат имеет
Таким образом, Ре (# 0 = Fe (J X, = s) = г- * (n8) ‘/ s!, B’) и для условной меры получить выражение л Ух, $ „(Х„ | # $) = е — »* Ъ а ‘/ \ пх, 1) (г-» »(лву / я! Г’ = ¦¦ «С) Людмила Фирмаль
Номинальная вероятность в), а общий опыт приводит к результатам (.V |, n, … xn) вероятность A). Итак, с точки зрения Информация о параметре 8 важна только в начале Обозначенный двухэтапный опыт, результат Статистика с ,,. (Болезнь) ?? = {x ,, = (a — ,,. Y2, ….. v- ,,):. V, = l, 2, …, / V, i = l, 2 … •••, n), P; v (x ,.) = N ~ n, XjigI1, т.е. речь идет о выборке с возвратом Возвращает кость n с L номером ball. параметр Принимает природную ценность. Условное распределение Если X (H) = m, распределение зиборн X является пара Параметр V. = m) = ^ n (* (»> N (Xn-xn | X (n) = t) = #. V (Xn = xn IP (X (n) = вкл) = Аргументы, похожие на предыдущий пример
Статистика * („> Параметры W доступны в образце. 3. Достаточно статистики: определение. (??, SS, {P}) как дискретная статистическая модель. Множество $ конечно или счетно, SS — система всех подмножеств 8В. В этом случае числовая функция 7 «(х) Очевидно, вы можете измерить 9S. Другими словами, это статистика. для Любое P nz {P} семейства и заданное (вообще говоря, векторное (не) Статистика T (x) определяет семейство условных мер P *. Любой б3 и P4 (B) = P (BP <x: T (x) = t}) / P ([x: T (x) = t}), D) Где Pe {P} и индекс t конкретного P выполняют все множества Г) ненулевой знаменатель. Определение 1. Статистика T (x) называется достаточно
Для дискретных статистических моделей (SB, 9S, {P}) Каждая t-условная мера вероятности P * не зависит от Pe s {P}. Примечания 1. Для каждого t обратите внимание на следующее. Вообще говоря, существует подмножество множества мер P {P} Знаменатель уравнения D) не равен нулю, т.е. Для этих Ps условные меры P * должны соответствовать друг другу. Более показательным является случай параметризованной семьи {P (b в ev), где определение достаточности T (x) полезно. 123 Сформулируйте следующее: существует семейство измерений P * Из индекса т Pe (B {{x: T (x) = t}) / Pe ({x: T (x) = t}) — P * (B) Da Левая сторона с Да) определяется. Замечание 2. Используя тот факт, что D) Образец частичного пространства вместо условной меры [S6, &) Введите условные вероятности т) Д6)
Приведено достаточно определений статистики T (x) как статистики Условная вероятность D6) независимо и на пределе Внутри семьи {5 *} (для некоторых D6) определяется). Из определения достаточной статистики T (x) В приведенном выше примере статистика T (x) содержит все Примерная информация x, чтобы помочь отличить элемент P Из {P}. Но понятие информации не формализовано Значимое значение сказанного является искусственным Искусственное моделирование образцов Xm с распределением R. Повторите это Общий вывод дела. Во-первых, реализовать следующий опыт Элемент Pe {P} моделирует (вообще говоря, вектор) по ели. с. Т.А. P (Tα = t) = P (T (X) = t) E)
Тогда по значению съедено. с. TL) и дано Построить главную семью П *. с. Xm со многими значениями {x: T (x) = t} и вероятность = 1) = p ‘(x). F) Умножьте E) и F) и примите во внимание D) То есть Xm имеет то же распределение, что и X, Поскольку первый шаг в моделировании зависит от Pe {P}, Различают элемент P и информацию {P}. Результат Тм Ясно, что первая стадия — это T <V1 = = T (XL |), T (x) считаются достаточной статистикой. Поэтому в искусственных экспериментах достаточно статистики Т (х) Является носителем всех полезных идентифицирующих элементов P. {P} информация. Определение 2. Достаточная статистика S (x) называется Минимум, если может быть выражен как (векторная) функция
Достаточно статистики.Видимо интерес к статистике актуален Возможность уменьшить ненужную информацию, содержащуюся Образец, тем самым продвигая последующие возможности Анализ. Следовательно, из достаточной статистики T (x) Храните достаточно свойств в статистике (T (x)), Где функция ij> (t) принимает то же значение для некоторых * Если 1 = / ^ 2, статистика ^> (T (x)) имеет приоритет над T (x). Из определения Как только вы определили достаточно минимальной статистики, Невозможно дальнейшее сокращение данных без потери необходимой информации Невозможно.
Статистика, описанная в примере (I) — (III) достаточно. использование Предварительные рассуждения. 77x) как достаточная статистика для дискретной модели ($?, Λ, {Pb}) и / | = / = で す означают два. Давайте перейдем к статистике Статистика \ fG «(x)), где if (/) ss / fort \ = f = tt и $ (t2) = ti, т.е. статистика \ fG (x)) соответствует 7 «(x), потому что последний значение, исключая / r и 7 «(x) = ^ выборок 7 «(х) = фи. Эти сокращения данных поддерживают достаточные характеристики. какие Чтобы это произошло, условная вероятность = х. R (x) = f. ) -У Г) Не должно зависеть от 6 (для 6 в уравнении G) Имеет смысл). Преобразовать числитель в G, используя условное выражение
Вероятность: 1 = 1,2. (8; Статистика 7 «(х) для достаточности условной вероятности (8) Зависит от параметра 6 (см. Да). Будь лаконичен (?!> E (X = x | r (X) = f <) = / JI- (x), t = 1,2, и переписать условие В виде вероятности г) q (() U Pr (x) + (A (x) -Pl (x)) c? > 9 (T (X) = <1) C-cU> 9 (T (X) Уравнение (9) не зависит от 6 (в котором знаменатель равен (9) не равен нулю) p1 (x) var2 (x), т.е. Пример распределения значений i \ и h с достаточной статистикой 7 «(x) равно или одинаково, или коэффициент p2 (x) -pi (x) в (9) равен Зависит от 0. Соотношение c * ”в (T (X) = tt) P9 ({x: T (x) = M) c * ”в (T (X) = h) = Pb ({x: T (x) = м2, принять значение Ноль для m \ минимальна. 4. Достаточные стандарты. Рассмотрим параметрическую модель для наглядности (X, A, {Rd, 8ev)).
Сделайте T (x) достаточной статистикой. по Put * (T; 6) = Pe ({x: T (x) = t}). Основные отношения Da) можно записать в виде: в), t = T (x). Введя функцию A (x) = PT (x) (x). Мы получаем в) А (х), немного 7. A1) Разработка модели распределения вероятностей Pb (x) C7, o8, {P9: ve6}) A1) Фактор A (x) не зависит от 0e6, другой зависит от x В терминах статистики T (x) мы называем это факторизацией распределения Распространение. Факторизация P0 (x) уникальна. Например, prop: vi: функция, которая не исчезает φ (x) и настройка , А ‘(х) 126 Получить из А1) Pv (*) = Очевидная факторизация всегда возможна. Pb (x) = Pb (x) -1 Следовательно, если статистика T (x) достаточна, коэффициент Разложение А1).
Обратное утверждение верно. Предположим, что есть разложение A1). Здесь, T (x) — некоторая статистика, g (t; 6) — функция от t, f (x) — Функция не зависит от 0. Статистика Т (х) В таком случае этого достаточно. Все меры Pfl были рассмотрены Установите нули {x: A (x) = 0}, эти x Дальнейшее рассмотрение. От А1) ); C) A (x) = = * (T; c) y. А (х). A2) x € B, T (x) = t Из а2) если б = я Pe ({x: T (x) = t »= * (t; c)? A (x) .A3) Т (х) = т Put P ‘(B) =? A (x) /? А (х). x6B.T (x) = t T (x) = t Если PQ ({x: T (x) = tj)> 0, A2) делится на A3), то 6 Поскольку условная мера соответствует P ‘(B), Статистика T (x) достаточна.
Следовательно, получены Теорема факторизации. Делать статистику T (x) — дискретная модель (9B, J &, {Po: 0 «= ev}); необходимо и достаточно для выполнения факторизации Разложение А1). При правильном изменении обозначений, то же самое Результаты явно верны для параметрических моделей. Найти достаточно статистики, используя Также „„ = 1. Мера вероятности Pb> 0 <0 <1 формула Где L ‘(x) — число координат вектора x. По теореме фактор Факторизация W (x) является достаточной статистикой. 5. Достаточно и достаточно минимальные перегородки. Статистические данные Ti (x) и T2 (x), относящиеся один к одному Преобразованием m / (x) = \ J> (T2 (x)) называется эквивалент.
обор Эквивалентная статистика содержит ту же информацию о статистике. Статистическая модель. Достаточно, если одного из них достаточно Там будет другой. Каждый из них является сокращение данных Статистика та же: система подмножеств {x: T, (x) -t,} и {x: T2 (x) «t2}, Где ti и t2 проходят через их соответствующие наборы значений Статистика Ti и T2 одинаковы. Определение 3. Разбиение множества SS на подмножества Подмножество 951, где t выполняется для нескольких наборов индексов. [) T t, 0 T Вызывается достаточно для дискретных моделей (I?, SB, {P}). Для условных мер Независимо от Pe {P} (для определенного t из P, P (I? H) ))) Если у вас есть достаточно расколов,
Числовые константы функции могут быть определены для элементов Создайте разделы и примите разные значения и разные элементы Элемент. Для этой функции достаточно статистики. Хорошо иметь Элементы разбиения {«Y *} множества СС в целом Достаточно элементов раздела {SSt} Среди произвольных a существует t = ta, такое как VaE. Достаточно На самом деле, если xe 0, отношения Pb (x) / Pb (y) независимы Для всех G зависит от G и равно либо Pg (x), либо Pd (y) Ноль, также эквивалентный пулям. Соотношение х / у очевидно Рекурсивно: xRx применяется к любому x. Симметрия: если х / б? у, то у /? И x, и переходные: xRy, yRz => xRz.
Вот так xRy — это отношение эквивалентности, как вы знаете, Me? $ V разбивается на непересекающиеся классы X = \ iXt, HW.-S, 5ph (, A4) T Где / выполняется на нескольких наборах индексов, каждый Класс 95i состоит из набора всех элементов, эквивалентных R эквивалентны друг другу. Заявление. Сделайте hey1 необязательным. Обозначается Множество всех элементов y, которые являются xRy. Тогда xRx, следовательно, Поэтому XeUh. Допустим, ЗГ произвольно [\ uf Ф2>, есть элемент от пересечения. с того времени xRu и zRu, то симметрия u /? z, и переходный xRz. делает \ ^ Yx, то zR \, так как xRz, транзитивным xRv, То есть ve ^ i или VxEif * -get Y% E.Yy аналогичным образом. Yx = Yx, следовательно, подмножество системы Yx xe3? Любые два из них не пересекаются или не совпадают.
Определения Для Vx, -Vx и f определите функцию f = f (x) такую, что f (xi) = f (x2). ‘(Си) =? / (X2) если установлено Set = 0 Если такого 0 не существует Если присутствует, положите i | — (f, x, y) = oo. Определение A5) является Правильный ответ. Если все 0 e Pb (x) = 0, все в порядке. Функция φ однозначно определена и принимает значение oo. Пусть 0i Пгт (х)> 0 и т. Д. Далее, согласно определению класса S6t, 5 М.В. Козлов. А.В Прохоров 11 Для всех восьми таких, что Pq (Y)> 0 и P0 (x)> 0, равенство По мере необходимости. Исправить 0eE Это было исправлено.
Предположим, что P0 (j? /)> O и Pfl (x)> 0. По определению Все P0 (y)> 0 класса 861 в этом случае суммируются А5), получить /, Х) =? ! > (, X, y) = Pb (x,) / Pb (x). 6 ¦ ”/ Откуда А6) Рассуждение справедливо для всех Pe (x)> 0. Если 0, P0 (x) — если 0, Определение класса 8B t также PQ (& t) = 0. Таким образом, A6) P0 (j? <)> O и раздел Раздел А4) достаточно. Доказать минимальность разбиения А4) Достаточно ли разделов (Va) и V (x) Сгенерированный раздел {^ aj имеет достаточно статистики (V (x) — любой Любая функция, которая принимает разные значения на разных Элементы перегородки).
По теореме факторизации Pe () = * (V (x); c) A (x). Далее ограничить подмножество 8? = {x: li (x)> 0), это Включает поддержку всех основных P0 (x). х, уу ^ «сделать так V (x) = V (y) = v тогда P0 (x) = g (v; c) A (x). Pe (y) = * (v; c) A (y). Если g (\; 9) = 0, Po (x) = Po (y) = 0. Если g (\ -c)> 0, Таким образом, x, y принадлежат по отношению к R Один элемент А4) для перегородок достаточно. Итак, стихия Раздел { 0} <= {jc: P0 (x)> 0}. A7) Выполните дальнейшую настройку с подмножеством SS ‘= = {x: Po (x)> O} s #? Статистика показывает T (x) = (P, (x) / P0 (x), P * (x) / Pn (x)) Минимума достаточно. х, да #? Принадлежит Один элемент А4) с достаточно минимальными перегородками.
В этом случае отношение P, (x) / P * (y) не зависит от i для всех i. P .- (x), P, (y)> 0, остальные — i P, (x) = P, (y) = 0 В результате R. (x) / P. (Y) = Po (x) / Po (y), Или P, (x) = P, (y) = 0. Во всех случаях P «(x) / Po (x) = P, (y) / Po (y) Таким образом, для всех i = 1, …, k, т. Е. T (x) = T (y), элемент Раздел, порожденный статистикой T (x), имеет с * 131 Полицейский с минимальным разделом (сужается SB ‘) Следовательно, T (x) является минимально достаточной статистикой. Установите, если условие A7) не выполняется (-0 Найти статистику T (x), где Po (x) заменяется на Po * (x), легко Оказалось, что минимума достаточно. Вывод любой семьи {Pfl: 8e0} Он остается неизменным при следующих условиях: A7).
Достаточно разделов генерируются системой статистики, Зависит от 6 как параметры: Ch; c) = Re (x), девятый в. A8) Если множество конечно, A8) можно рассматривать следующим образом: Векторная статистика. В общем, для краткости, система А8) называется функциональной статистикой. На каждом фиксированном Исправлено 0 = «координаты; -L (x; 9») — нормальный скаляр Статистика, всего таких координат Составьте функциональную статистику A8). Достаточно маленький раздел генерируется функцией Функциональная статистика 7 (x; 9) = L (x; 9) / L (x; в „), 9 <= в,
Где 9ev для всех 9ev {x: Pb (x)> 0} и {x: Pv. (X)> 0}. В примере (II) выборка из распределения Пуассона N L (x; 9) / L (x; 90) =. e — «<ооо.> @ / 0o) га Получить после входа N In (L (x; 6) / L (x; 60)) = -nF-c,) + J] In In (Lj.A9) Поскольку взаимно-однозначное преобразование эквивалентно, Эквивалентная статистика, то А9) тоже минимальная Как видно из А9), «координаты» фу
Смотрите также:
| Статистическая модель | Определение достаточной статистики, теорема факторизации |
| Подобные статистики | Экспоненциальные семейства, минимальная достаточность |
Если вам потребуется помощь по статистике вы всегда можете написать мне в whatsapp.

