Свойства определенного интеграла
1. 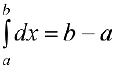
2. Пусть функции 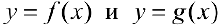 — интегрируемы на
— интегрируемы на 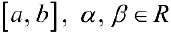 , тогда
, тогда 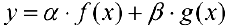 — также интегрируема на
— также интегрируема на 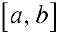 и
и 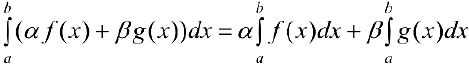 (линейность интеграла).
(линейность интеграла).
Доказательство. По формуле (1):
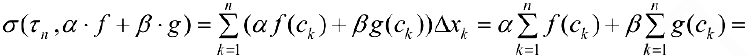
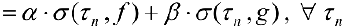 . По формуле (3):
. По формуле (3):
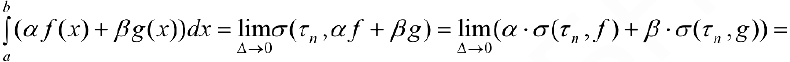
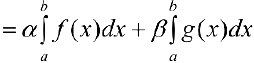 , что и требовалось доказать.
, что и требовалось доказать.
3. Аддитивность интеграла. Если функция 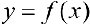 интегрируема на отрезке
интегрируема на отрезке 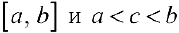 , то
, то 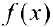 интегрируема на
интегрируема на 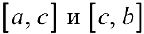 и
и
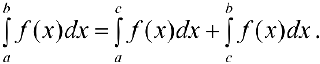
Верно и наоборот.
Доказательство. Так как 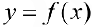 — интегрируема на
— интегрируема на 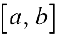 , то она ограничена на
, то она ограничена на 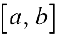 ( теорема 1) и, следовательно, ограничена на отрезке
( теорема 1) и, следовательно, ограничена на отрезке 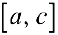 и
и 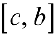 .
.
Пусть 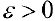 и
и 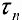 разбиение
разбиение 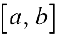 такое , что
такое , что 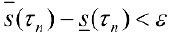 (см. формулу (6)). В разбиение
(см. формулу (6)). В разбиение 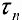 можно добавить точку с, если ее там нет, при этом полученное разбиение также будет удовлетворять неравенству (6). Тогда
можно добавить точку с, если ее там нет, при этом полученное разбиение также будет удовлетворять неравенству (6). Тогда
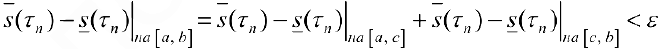 , поэтому и ограничение разбиения
, поэтому и ограничение разбиения 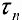 на
на 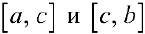 будут удовлетворять неравенству (6) и, следовательно (см. соотношение (6)),
будут удовлетворять неравенству (6) и, следовательно (см. соотношение (6)), 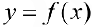 будет интегрируема на
будет интегрируема на 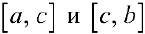 . Будем измельчать разбиение
. Будем измельчать разбиение 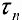 так, чтобы
так, чтобы 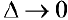 :
:
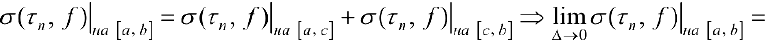
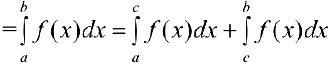 что и требовалось доказать.
что и требовалось доказать.
4. Пусть 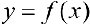 — интегрируема на
— интегрируема на 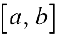 и
и 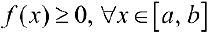 , тогда
, тогда 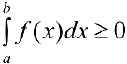 .
.
Доказательство. 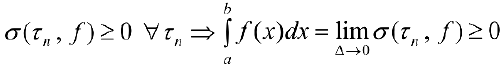 .
.
5. Пусть 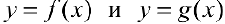 — интегрируемы на
— интегрируемы на 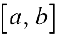 и удовлетворяют неравенству
и удовлетворяют неравенству 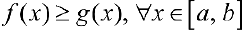 , тогда
, тогда 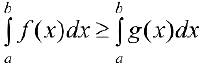 .
.
Доказательство.
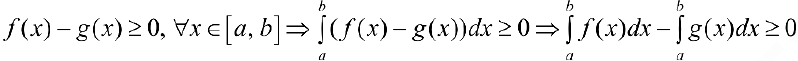
6. Пусть 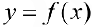 — интегрируема на
— интегрируема на 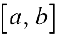 , тогда
, тогда 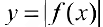 — также интегрируема на
— также интегрируема на 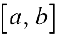 и
и
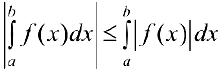
Доказательство следует из неравенства 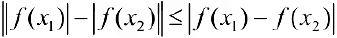
7. Пусть 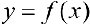 — интегрируема на
— интегрируема на 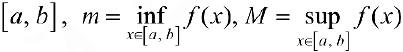 , тогда
, тогда 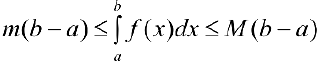
Доказательство, 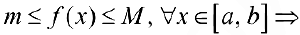 по свойству 5:
по свойству 5:
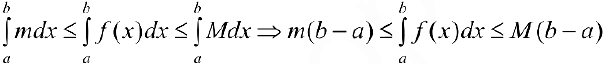
8. Пусть 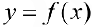 — непрерывна па
— непрерывна па 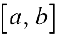 . тогда
. тогда 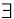 точка
точка 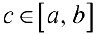 такая, что
такая, что
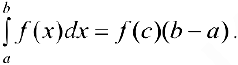
Доказательство. Так как 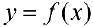 — непрерывна, то опа достигает на
— непрерывна, то опа достигает на 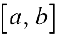 своей точной верхней М и нижней m граней (теорема 1 §11). Тогда из формулы (9) следует, что
своей точной верхней М и нижней m граней (теорема 1 §11). Тогда из формулы (9) следует, что
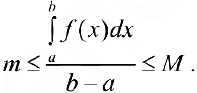
Так как 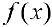 — непрерывна, то из т.2 § 11 следует,
— непрерывна, то из т.2 § 11 следует, 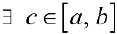 такая, что
такая, что 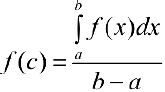 , что и требовалось доказать.
, что и требовалось доказать.
Замечание. Число 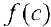 называется интегральным средним значением функции
называется интегральным средним значением функции 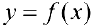 на отрезке
на отрезке 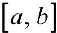 . Если
. Если 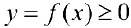 , то согласно примеру 2
, то согласно примеру 2 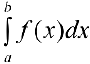 равен площади
равен площади 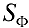 фигуры
фигуры 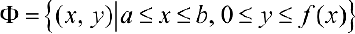 .
.
Из формулы (10) следует, что эта площадь равна площади прямоугольника высотой 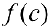 с основанием
с основанием 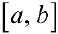 :
:
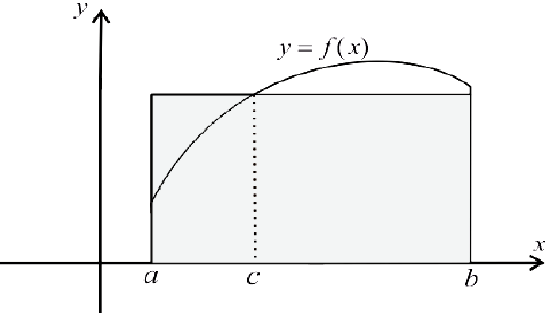
Рис.6. 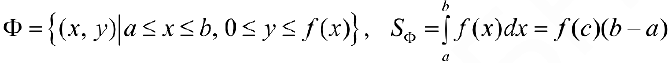
Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:
Решение задач по математическому анализу
Возможно эти темы вам будут полезны:

