Задача 2.64.
Для всех значений параметра 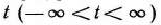 найти максимальное значение функции
найти максимальное значение функции
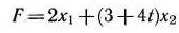
при условиях
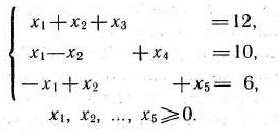
Решение:
Считая в целевой функции исходной задачи значение параметра 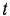 равным 0 (число 0 взято произвольно), находим симплексным методом ее оптимальный план
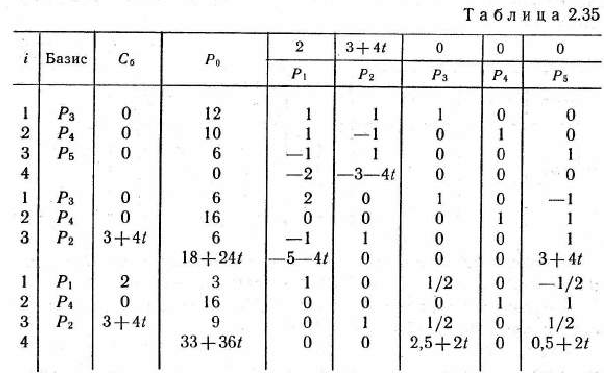
равным 0 (число 0 взято произвольно), находим симплексным методом ее оптимальный план 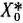 =(9; 0;16; 0) (табл. 2.35). После этого определяем значения параметра I, для которых
=(9; 0;16; 0) (табл. 2.35). После этого определяем значения параметра I, для которых 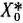 J=(3; 9; 0; 16; 0) остается оптимальным планом. Очевидно, это будет тогда, когда среди элементов 4-й строки последней симплекс-таблицы (кроме элемента, стоящего в столбце вектора
J=(3; 9; 0; 16; 0) остается оптимальным планом. Очевидно, это будет тогда, когда среди элементов 4-й строки последней симплекс-таблицы (кроме элемента, стоящего в столбце вектора 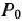 ) не будет отрицательных, т.е. при
) не будет отрицательных, т.е. при 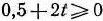 и
и 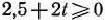 , откуда
, откуда  . Итак, если
. Итак, если 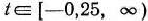 , то задача (74) — (76) имеет оптимальный план
, то задача (74) — (76) имеет оптимальный план 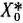 = (3; 9; 0; 16; 0), при котором
= (3; 9; 0; 16; 0), при котором 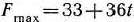 .
.
Возьмем теперь некоторое значение параметра 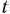 , меньшее чем —0,25. Тогда элемент, стоящий в 4-й строке столбца вектора
, меньшее чем —0,25. Тогда элемент, стоящий в 4-й строке столбца вектора 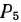 последней симплекс-таблицы (табл. 2.35), станет отрицательным. Следовательно, приданном значении параметра
последней симплекс-таблицы (табл. 2.35), станет отрицательным. Следовательно, приданном значении параметра 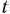 план
план 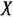 = (3; 9; 0; 16; 0) не является оптимальным. Поэтому переходим к новому опорному плану, для чего исключим из базиса вектор
= (3; 9; 0; 16; 0) не является оптимальным. Поэтому переходим к новому опорному плану, для чего исключим из базиса вектор 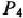 и введем в него вектор
и введем в него вектор 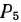 (табл. 2.36).
(табл. 2.36).
Полученный новый план 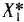 =(1; 0; 0; 16) является оптимальным при
=(1; 0; 0; 16) является оптимальным при 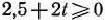 и
и  , т.е. при
, т.е. при 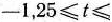 0,25. Таким образом, если
0,25. Таким образом, если 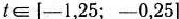 , то задача (74) — (76) имеет оптимальный план
, то задача (74) — (76) имеет оптимальный план 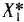 =(11; 1; 0; 0; 16), при котором
=(11; 1; 0; 0; 16), при котором 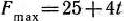 .
.
Найдем теперь решение задачи при 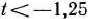 . В этом случае элемент, стоящий в 4-й строке столбца вектора
. В этом случае элемент, стоящий в 4-й строке столбца вектора 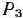 табл. 2.36, отрицателен. Следовательно, записанный в таблице опорный план не является оптимальным. Переходим к новому опорному плану, для чего исключим из базиса вектор
табл. 2.36, отрицателен. Следовательно, записанный в таблице опорный план не является оптимальным. Переходим к новому опорному плану, для чего исключим из базиса вектор 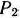 и введем в него вектор
и введем в него вектор 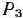 (табл. 2.37).
(табл. 2.37).

Полученный опорный план является оптимальным для любого 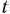 такого, что
такого, что 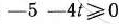 , т.е. для
, т.е. для  .
.
Следовательно, для 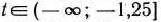 исходная задача имеет оптимальный план
исходная задача имеет оптимальный план 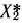 =(0; 2; 0; 16), при котором
=(0; 2; 0; 16), при котором 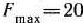 .
.
Итак, если 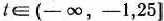 , то задача (74) — (76) имеет оптимальный план
, то задача (74) — (76) имеет оптимальный план 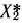 =(10; 0; 2; 0; 16), a
=(10; 0; 2; 0; 16), a 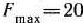 ; если
; если 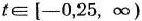 , то
, то 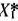 = (11; I; 0; 0; 16) — оптимальный план, а
= (11; I; 0; 0; 16) — оптимальный план, а 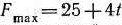 ; если
; если 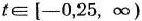 , то
, то 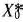 = (3; 9; 0; 16; 0) — оптимальный план, a
= (3; 9; 0; 16; 0) — оптимальный план, a 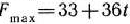 .
.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:

