Задача 2.17.
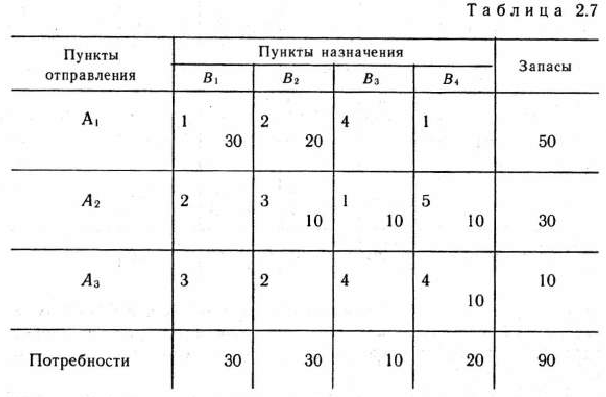
Для транспортной задачи, исходные данные которой приведены в табл. 2.7, найти оптимальный план.
Решение:
Сначала, используя метод северо-западного угла, находим онорный план задачи. Этот план записан в табл. 2.7.
Найденный опорный план проверяем на оптимальность. В связи с этим находим потенциалы пунктов отправления и назначения. Для определения потенциалов получаем систему
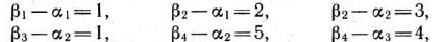
содержащую шесть уравнений с семью неизвестными. Полагая
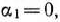
находим
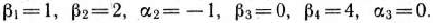
Для каждой свободной клетки вычисляем число
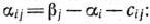
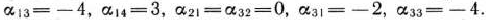
Заключаем найденные числа в рамки и записываем их в каждую из свободных клеток табл. 2.8.
Так как среди чисел 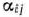 имеются положительные, то построенный план перевозок не является оптимальным и надо перейти к новому опорному плану. Наибольшим среди положительных чисел
имеются положительные, то построенный план перевозок не является оптимальным и надо перейти к новому опорному плану. Наибольшим среди положительных чисел 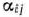 являются
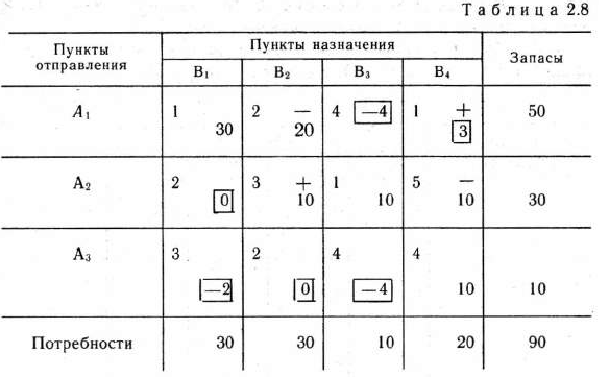
являются 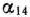 = 3, поэтому для данной свободной клетки строим цикл пересчета (табл. 2.8) и производим сдвиг по этому циклу. Наименьшее из чисел в минусовых клетках равно Ю. Клетка, в которой находится это число, становится свободной в новой табл. 2.9. Другие числа в табл. 2.9 получаются так: к
= 3, поэтому для данной свободной клетки строим цикл пересчета (табл. 2.8) и производим сдвиг по этому циклу. Наименьшее из чисел в минусовых клетках равно Ю. Клетка, в которой находится это число, становится свободной в новой табл. 2.9. Другие числа в табл. 2.9 получаются так: к
числу 10, стоящему в плюсовой клетке табл. 2.8, добавим 10 и вычтем 10 из числа 20, находящегося в минусовой клетке табл. 2.8. Клетка на пересечении строки 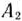 и столбца
и столбца 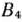 становится свободной.
становится свободной.
После этих преобразований получаем новый опорный план (табл. 2.9).
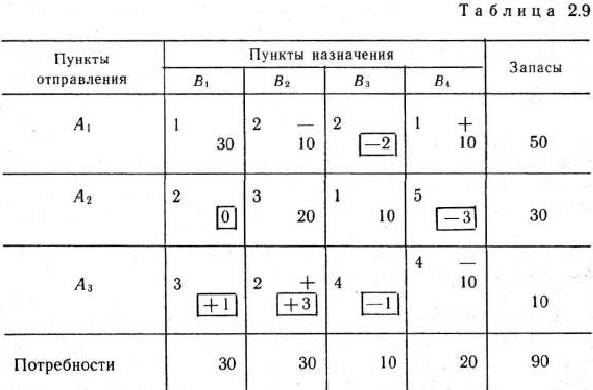
Этот план проверяем на оптимальность. Снова находим потенциалы пунктов отправления и назначения. Для этого составляем следующую систему уравнений:
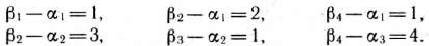
Полагаем

получаем
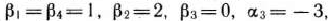
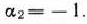
Для каждой свободной клетки вычисляем число 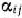 ; имеем,
; имеем,
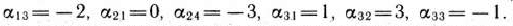
Таким образом, видим, что данный план перевозок не является оптимальным. Поэтому переходим к новому опорному плану (табл. 2.10).
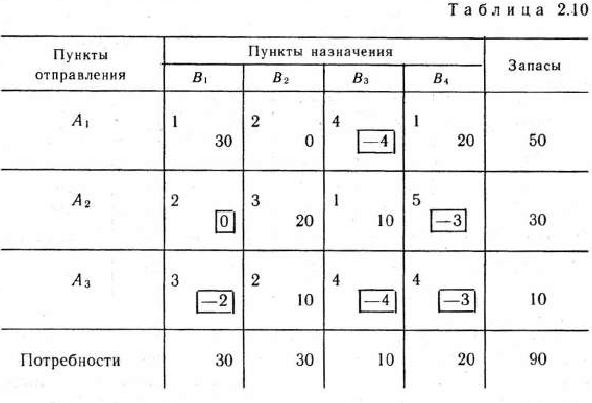
Сравнивая разности  новых потенциалов, отвечающих свободным клеткам табл. 2.10, с соответствующими числами
новых потенциалов, отвечающих свободным клеткам табл. 2.10, с соответствующими числами 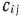 , видим, что указанные разности потенциалов для всех свободных клеток не превосходят соответствующие чисел
, видим, что указанные разности потенциалов для всех свободных клеток не превосходят соответствующие чисел 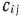 . Следовательно, полученный план
. Следовательно, полученный план

является оптимальным. При данном плане стоимость перевозок
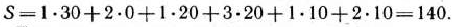
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:

