Задача №151.
Для ступенчатого чугунного бруса (рис. 10.9, а) определить из расчета на прочность допускаемую нагрузку, если площадь поперечного сечения в верхней части бруса равна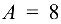 
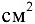, и в два раза меньше площади сечения в нижней части,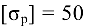 
.
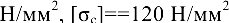Решение:
В данном примере все внешние силы действуют по одной прямой, поэтому можно составить одно уравнение равновесия, из которого будет найдена неизвестная реакция:
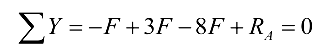
отсюда
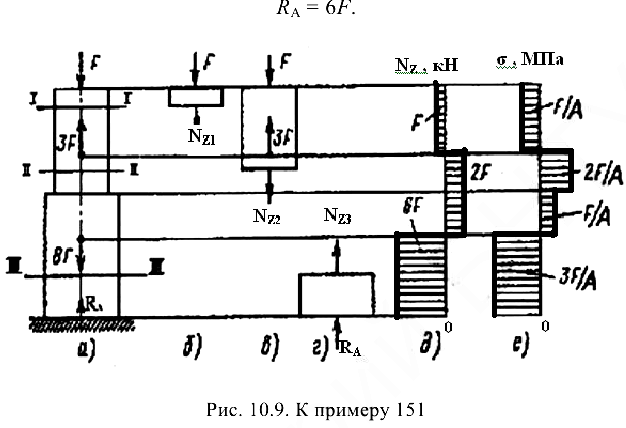
Построим эпюру сил. Для этого воспользуемся методом сечений. Проведем сечение I — I и отбросим часть бруса, лежащую ниже сечения (рис. 10.9, б). Вместо отброшенной нижней части приложим внутреннюю силу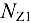 
. Если неизвестную продольную силу всегда направлять от сечения, т. е. предварительно предполагать, что брус на данном участке испытывает растяжение, то знак продольной силы, найденной из уравнения равновесия оставшейся части бруса, будет указывать не только на правильность или неправильность выбранного ранее направления, по и на вид деформации, т. е. на растяжение или сжатие. Запишем уравнение равновесия части бруса:
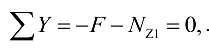
откуда
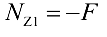
На участке от точки приложения силы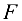 
до точки приложения силы 3 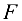мы придем к аналогичному результату независимо от того, где будет проведено сечение. Значит, на этом участке продольная сила постоянна. Сечение II — II проведем ниже точки приложения силы 3F и опять отбросим нижнюю часть бруса (рис. 2.9, в). Составляя уравнение равновесия, получим 
:
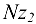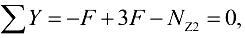
откуда
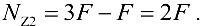
Следует заметить, что при составлении уравнений равновесия надо использовать правило знаков проекций сил, принятых в теоретической механике, а именно: проекция силы берется со знаком плюс, если ее направление совпадает с положительным направлением оси.
Определяя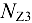 
, удобнее оставить нижнюю часть бруса, отбросив верхнюю (рис. 10.9, г):
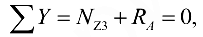
откуда
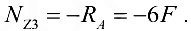
Построим эпюру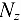 
. Для этого параллельно оси бруса проведем базовую линию. Левее базовой линии (линии нулей) будем откладывать продольную силу, вызванную сжатием участка, а правее — растяжением. В пределах каждого участка нагружения (в данном примере их три — между точками приложения внешних сил, включая силу реакции) продольная сила не меняется, поэтому эпюра будет очерчена прямыми, параллельными базовой линии. В произвольном масштабе отложим 
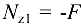. Так как па этом участке брус испытывает сжатие, то отложим 
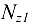левее базовой линии. На втором участке 
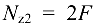отложим значение правее линии нулей, и, наконец, на третьем участке брус снова испытывает сжатие, поэтому 
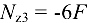отложим левее. Эпюра продольных сил построена (рис. 10.9, д).
Вспомним,что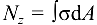 
. Используя гипотезу Бернулли, можно прийти к выводу, что при растяжении и сжатии напряжения равномерно распределены по всей площади поперечного сечения, т. е. для данного сечения
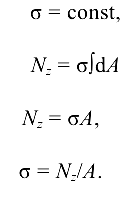
Зная продольную силу на каждом участке и площади поперечных сечений бруса, можно построить эпюру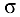 
(рис. 10.9, е). В произвольном масштабе откладываем влево и вправо от базовой линии напряжения в поперечных сечениях (правило знаков остается прежним), получим
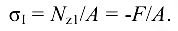
На втором участке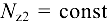 
, но скачкообразно меняется площадь поперечного сечения. Разделим этот участок на подучастки и определим напряжения:
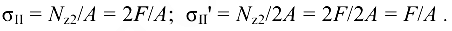
На третьем участке
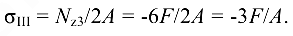
Брус выполнен из материала, различно сопротивляющегося растяжению и сжатию, поэтому допускаемое значение нагрузки надо найти как из условия прочности на растяжение, так и из условия прочности па сжатие:
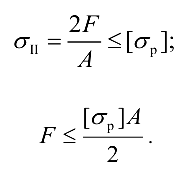
Подставим числовые значения и получим допускаемую нагрузку из условия прочности на растяжение:
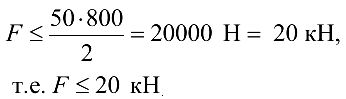
Запишем условие прочности на сжатие:
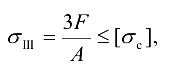
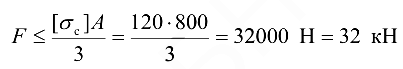
Окончательно мы выбираем то значение, которое удовлетворяло бы условию прочности как на растяжение, так и на сжатие, т. е.
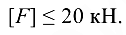
Если студент, приступая к решению задачи, имеет достаточный навык в построении эпюр, то при построении эпюры продольных сил нет необходимости изображать отдельно отсеченные части бруса, достаточно обратить внимание на то, что продольная сила, возникающая в произвольном сечении, равна алгебраической сумме всех внешних сил, приложенных к брусу по одну сторону от рассматриваемого сечения. Кроме того, при построении эпюр и проверке их правильности следует руководствоваться следующими правилами:
скачки на эпюрах 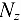имеют место в точках приложения сосредоточенных сил, причем величина скачка равна приложенной внешней сосредоточенной силе;
на эпюре 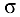скачки имеют место не только в точках приложения сосредоточенных сил, но и в местах резкого изменения площади поперечного сечения;
эпюра 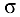по знаку должна совпадать с эпюрой .
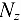Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:
