Задача 2.17.1
Для строительства трех дорог используется гравий из четырех карьеров. Запасы гравия в каждом из карьеров соответственно равны 120, 280 и 160 усл. ед. Потребности в гравии для строительства каждой из дорог соответственно равны 130, 220, 60 и 70 усл. ед. Известны также тарифы перевозок 1 усл. ед. гравия из каждого из карьеров к каждой из строящихся дорог, которые задаются матрицей
Составить такой план перевозок гравия, при котором потребности в нем каждой из строящихся дорог были бы удовлетворены при наименьшей общей стоимости перевозок.
Решение:
Исходные данные задачи сведем в таблицу (табл. 2.11).
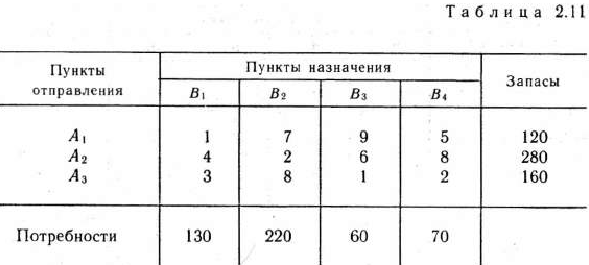
Как видно из табл. 2.1!, запасы гравия в карьерах (120 + 42804″ 160 = 560) больше, чем потребности в нем (130 4 220 + 4 604-70 = 480) на строящихся дорогах. Следовательно, модель исходной транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительный пункт назначения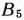 
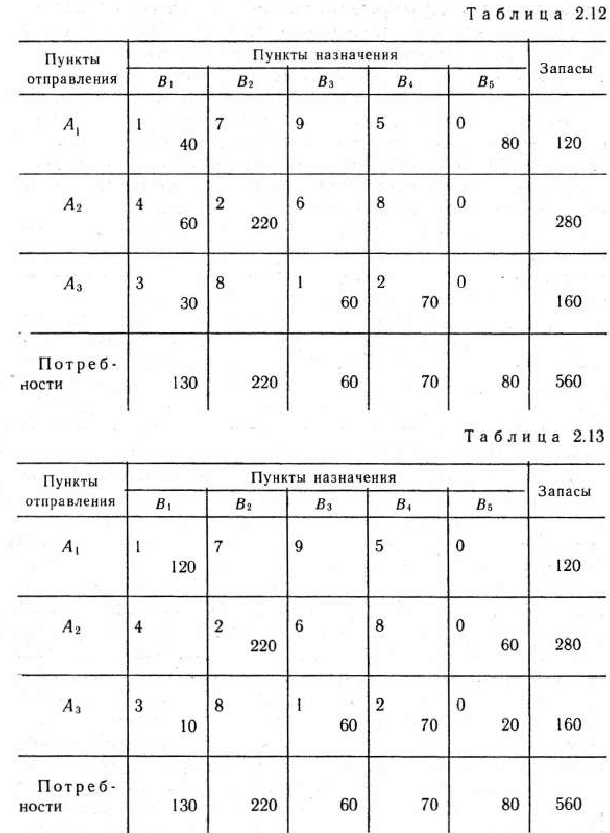
с потребностями, равными 560—480 = 80 усл. ед. Тарифы перевозки единицы гравия из всех карьеров в пункт 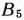полагаем равными нулю. В результате получаем закрытую модель транспортной задачи, план перевозок которой определяем методом минимального элемента (табл. 2.12).
Оптимальный план находим методом потенциалов (табл. 2.13).
Как видно из табл. 2.13, исходная задача имеет оптимальный план
При этом плане остается неиспользованным 60 усл. ед. гравия во втором карьере и 20 усл. ед. в третьем карьере, а общая стоимость перевозок составляет
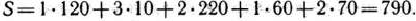
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
