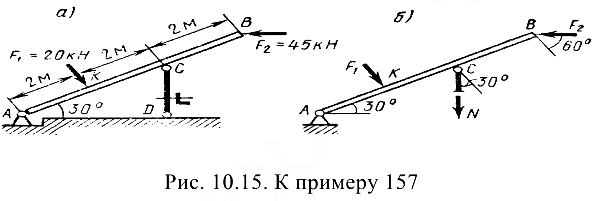
Задача № 157. (рис. 10.15, а).
Для стержня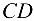 
, удерживающего в равновесии жесткую балку 
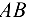и выполненного из равнополочного уголка, подобрать размеры сечения и определить удлинение (укорочение) стержня. Для материала стержня (сталь СтЗ) принять допускаемые напряжения при растяжении 
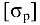= 160 МПа и при сжатии 
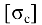= 120 МПа и модуль продольной упругости 
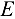= 200 ГПа.
Решение:
Как известно из статики, шарнирно закрепленный стержень может находиться в равновесии лишь при условии, что нагружающие его по концам силы расположены по продольной оси стержня. Поэтому в поперечных сечениях стержня возникает лишь один внутренний силовой фактор — продольная сила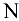 
, т. е. имеет место растяжение (сжатие) стержня.
Для определения продольной силы применяем метод сечений. Проводя сечение, отбрасываем закрепленную часть стержня и к оставленной части прикладываем продольную силу 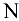, предполагая, что стержень растянут (рис. 10.15, б). Рассматриваем равновесие балки 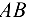. Применяя в качестве уравнения равновесия сумму моментов сил относительно центра опорного шарнира 
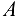(чтобы исключить из уравнения не подлежащие определению реакции шарнира), находим продольную силу :
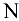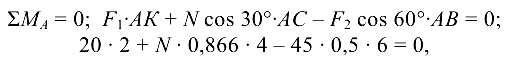
отсюда
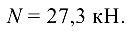
Знак плюс указывает на то, что стержень растянут. Из условия прочности стержня при растяжении определяем размеры уголка:
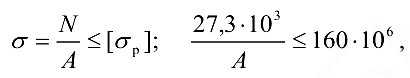
отсюда требуемая площадь
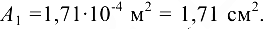
Здесь допускаемое напряжение
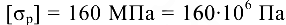
и продольная сила
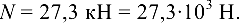
По таблице прокатной стали ГОСТ 8509 — 86 (прил.З) выбираем равнополочный уголок № 2,5, для которого
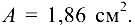
При выбранном размере уголка материал недогружен, однако незначительно (около 8 %).
Определяем удлинение стержня 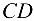, для чего применяем формулу Гука:
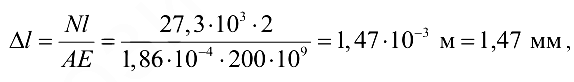
где площадь сечения
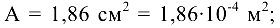
модуль продольной упругости материала
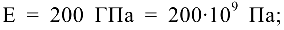
длина стержня
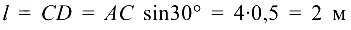
(определена из прямоугольного треугольника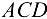 
).
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:
