Для построения схемы механизма заданного варианта прежде всего необходимо выбрать масштаб длин

Курсовая работа К3

Построение схемы механизма

Для построения схемы механизма заданного варианта прежде всего необходимо выбрать масштаб длин 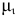, Например, если 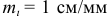, то это означает, что в одном миллиметре рисунка изображается 1 см натуральной длины звеньев и расстояний, в 10 мм — 10 см и т.д. По расстояниям , (см. табл. К2 а) следует отметить положения опорных точек. По значению угла 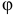(см. табл. К2 б) построить положение ведущего звена 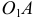. Затем по размерам других звеньев (см. табл. К2 а) построить окончательную конфигурацию механизма.

Если при построении механизма некоторые из указанных размеров звеньев окажутся меньше или больше необходимых, то их надо соответственно увеличить или уменьшить, учитывая в дальнейших вычислениях истинные размеры.

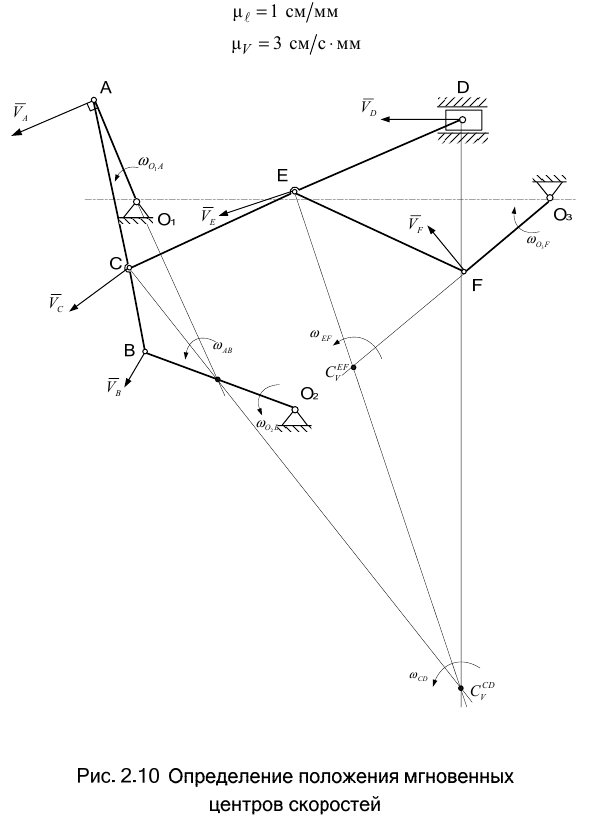
На построенной схеме механизма вокруг точки 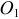следует показать круглыми стрелками направления угловой скорости 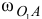и углового ускорения .

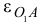На рис. 2.8 изображен механизм в масштабе , для которого

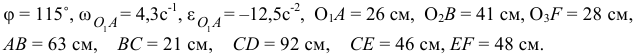
Вычисление скорости касательного, нормального и полного ускорений точки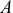

Скорость точки 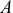звена 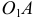определяем как линейную (вращательную) по формуле

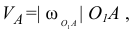
где 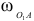— угловая скорость вращения ведущего звена ;

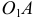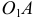— кратчайшее расстояние от точки 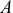до оси вращения.

По условию

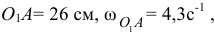
тогда

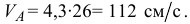
Вектор скорости точки 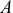перпендикулярен к 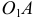и направлен в сторону вращения звена 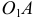(в сторону угловой скорости звена ).

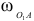Так как звено 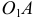вращается неравномерно, то точка 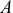будет обладать как нормальным, так и касательным ускорением.

Определим нормальное ускорение

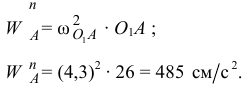
Вектор нормального ускорения точки направлен от точки 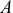к оси вращения 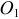вдоль звена 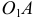. Касательное ускорение равно

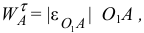
где 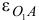— угловое ускорение звена .

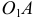По условию задачи

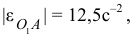
тогда

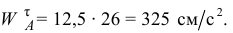
Вектор касательного ускорения точки 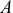направлен перпендикулярно вектору 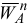, т. е. перпендикулярно звену 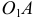в сторону углового ускорения 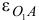звена 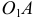. Полное ускорение точки 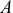найдём согласно формуле

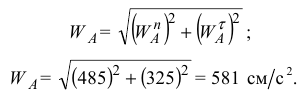
Построение плана скоростей и определение скоростей отмеченных точек механизма

Для построения плана скоростей плоского механизма необходимо знать модуль и направление скорости одной из точек механизма и прямую, по которой направлена скорость другой точки. При этом обе точки должны принадлежать одному звену механизма. В данном случае известна по модулю и направлению скорость точки .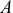

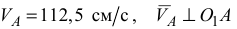
и направлена в сторону 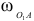. План скоростей строится в выбранном масштабе 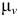вблизи от схемы механизма.

Последовательность построения плана скоростей

На схеме механизма (рис. 2.9), построенного в масштабе 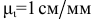, отложим от точки звена вектор 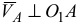в произвольном масштабе, направленный в сторону .

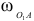Выбираем произвольную точку на чертеже (вблизи схемы механизма). Из этой точки в выбранном масштабе скоростей 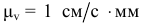проведем луч

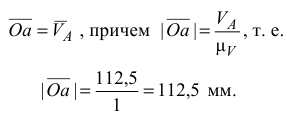
Затем, принимая точку за полюс, найдем скорость точки , направление которой известно . При этом воспользуемся теоремой о скоростях точек при плоскопараллельном движении твердого тела

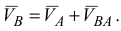
Согласно векторному равенству (1) проводим из точки плана скоростей прямую, параллельную направлению скорости , т. е. перпендикулярно звену , а из вершины а прямую, перпендикулярную звену 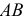, т. к. 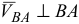. Пересечением двух прямых будет вершина 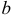плана.

Соединяя точку с вершиной , получим луч 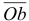, определяющий скорость точки т. е.

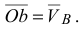
Измеряя луч 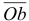и умножая его на масштаб 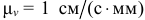, получим модуль скорости точки :

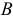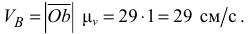
Скорость точки 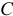определим, используя свойство пропорциональности отрезков плана скоростей соответствующим отрезкам плоского механизма, согласно которому составим пропорцию, позволяющую найти вершину с плана

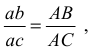
откуда

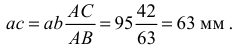
Отложив отрезок 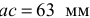на плане, определим вершину 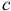. Соединяя точку 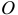с вершиной 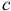, найдем луч 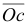, определяющий скорость точки 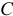, т. е.

Модуль скорости точки определим, измерив луч и умножив его на масштаб :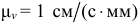

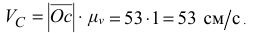
Затем рассмотрим звено 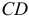, точка 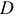которого движется вдоль горизонтальных направляющих, поэтому скорость 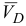направлена по горизонтали. Принимаем точку 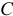за полюс и скорость точки 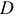найдем по формуле

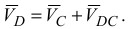
На основании векторного равенства (2) проводим из точки 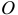плана горизонтальную прямую, соответствующую направлению 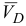. Поскольку 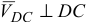, то из вершины с плана проводим прямую, перпендикулярную 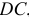, соответствующую направлению вектора 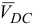. Пересечение двух прямых обозначим вершиной 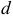. Проведем из точки 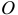в вершину 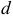луч 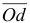, который определяет скорость точки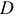

Измерив полученный луч 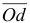, через масштаб скоростей 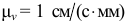получим модуль скорости точки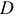

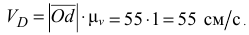
Скорость точки 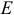вычислим аналогично определению скорости точки 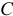. Для этого составим пропорцию, из которой найдем вершину 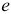плана

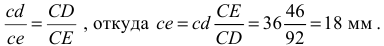
Отложив отрезок 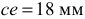на плане, определим вершину 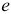. Из точки 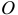в вершину 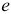проведем луч 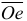, который определяет скорость точки т. е.

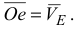
Измеряем луч 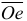и через масштаб скоростей вычисляем модуль скорости точки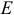

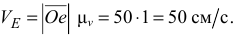
Далее рассмотрим звено 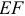и, принимая точку 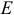за полюс, запишем:

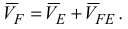
Скорость точки 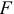известна по направлению 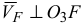, т. к. Звено 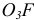вращается вокруг неподвижной оси, проходящей через точку 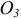. Зная это и следуя зависимости (3), проведем из точки 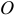плана прямую, перпендикулярную звену 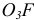, соответствующую направлению скорости точки 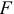. Из точки 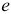проведем прямую, перпендикулярную звену 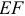, что соответствует направлению вектора 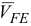, т.к. .

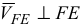Пересечение проведенных прямых определит положение вершины 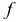плана. Из точки 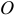проведем в вершину 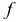луч 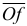, который определяет скорость точки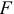

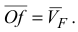
Модуль этой скорости вычислим через масштаб скоростей 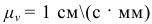, измерив луч .

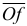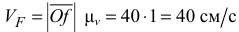
Определение положения мгновенных центров скоростей, угловых скоростей звеньев механизма и скоростей всех отмеченных точек

Схема механизма при этом построена в положении, соответствующем заданному, в выбранном масштабе 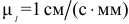(рис. 2.10). Для определения положения мгновенных центров скоростей звеньев механизма воспользуемся способами определения мгновенных центров скоростей, рассмотренных в краткой теории.

Чтобы определить положения мгновенного центра скоростей, достаточно знать направления скоростей каких-нибудь двух точек, а для определения скорости любой точки тела надо знать модуль и направление скорости какой-нибудь одной точки.

Найдем последовательно положение мгновенных центров скоростей звеньев 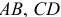и 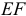, совершающих плоскопараллельное движение. Скорость точки 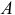звена 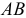была найдена ранее по модулю и направлению (см. П.2 примера выполнения) .

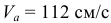Вектор 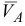направляем перпендикулярно звену 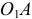в сторону угловой скорости 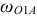в произвольном масштабе.

Точка В является общей точкой звена 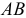и 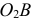. Так как звено 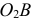совершает вращательное движение вокруг неподвижной оси, проходящей через точку 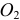перпендикулярно плоскости движения (плоскости чертежа), то вектор скорости точки 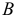, как скорости вращательной, направлен перпендикулярно звену 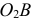. Проводим из точки 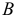прямую перпендикулярную звену 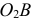. Затем из точек 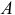и 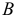проводим перпендикуляры к направлениям скоростей этих точек, которые пересекутся в точке 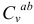определяющей положение мгновенного центра скоростей звена 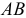. В данный момент времени звено 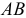вращается вокруг этого центра и скорости точек определяются как вращательные вокруг оси, проходящей через мгновенный центр скоростей перпендикулярно плоскости движения. Угловую скорость вращения звена 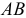определим по формуле 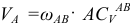, откуда .

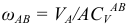Измеряя на схеме механизма длину отрезка 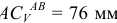и умножая на масштаб длин 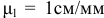, получим истинное значение отрезка 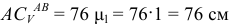. Окончательно получим .

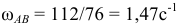Показываем круглой стрелкой направление 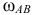вокруг точки 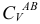в соответствии с известным направлением скорост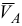и точки .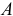

Зная 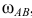, можно определить скорость любой точки звена 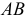по модулю и направлению.

Определим скорость точки

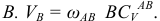
На схеме механизма 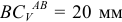. Истинное значение определим через масштаб длин

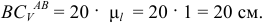
Тогда

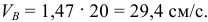
Направляем вектор 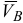перпендикулярно отрезку 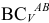в сторону угловой скорости 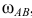. Рассматривая звено 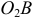, определим его угловую скорость вращения вокруг оси 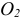. Так как 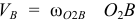, то отсюда

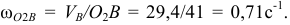
направление 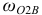показываем круглой стрелкой вокруг точки 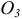в соответствии с направлением вектора .

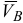Далее рассмотрим следующее звено 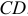. Надо определить направление скоростей точек 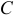и 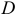. Точка С находится также на звене 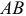. поэтому соединяем точку 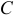с мгновенным центром скоростей 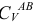звена 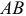и находим скорость по модулю по формуле

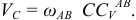
Замеряем отрезок 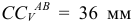на схеме, определяем истинное значение через масштаб длин

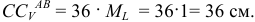
Окончательно получим

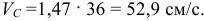
Вектор 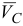проводим из точки 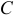перпендикулярно отрезку 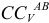, направленному в сторону угловой скорости 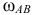звена .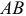

Направление скорости точки 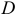известно — это горизонтальная линия. Проводим теперь из точек 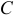и 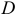перпендикуляры к направлениям их скоростей, на пересечении которых определится положение мгновенного центра скоростей 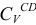звена .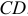

По аналогии с вышеизложенным найдем угловую скорость 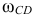звена

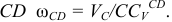
Измеряем на схеме 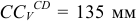и через масштаб длин находим истинное значение 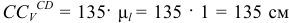и угловую скорость звена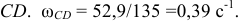

Скорость точки 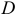по модулю определится

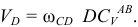
На схеме отрезок 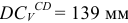и действительное значение его равно 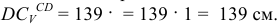Тогда

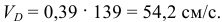
Вектор 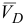длиной 54,2/3 = 18 мм проводим из точки 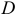вдоль горизонтальной линии в сторону угловой скорости 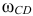звена .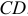

И, наконец, рассмотрим звено .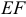

Скорость точки находящейся на звене 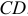, по модулю и направлению определим, соединив ее с мгновенным центром скоростей 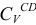звена

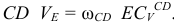
Замеряем на схеме 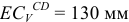. Истинное значение отрезка

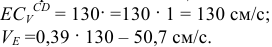
Вектор 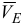направляем перпендикулярно отрезку 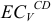в сторону угловой скорости 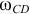звена .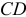

Точка 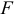принадлежит также звену 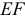, которое вращается вокруг неподвижной оси 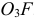. Значит, вектор 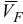как вращательная скорость направлен перпендикулярно звену 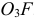. Проводим это направление из точки .

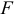Затем из точек 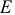и 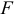проводим перпендикуляры к направлениям скоростей этих точек до их пересечения в точке 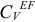, которая является мгновенным центром скоростей звена .

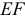Определяем теперь

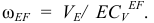
Измеряем на схеме отрезок 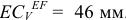. Находим действительное значение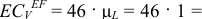 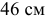. Подставляя значения, находим:

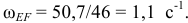
Теперь определим по модулю скорость точки 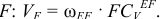Замеряем на схеме отрезок

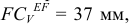
находим действительное значение

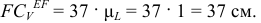
Затем определим

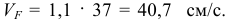
Вектор 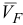направляем перпендикулярно отрезку 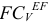в сторону угловой скорости звена .

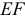Рассмотрим звено 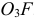и определим его угловую скорость 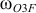. Для чего найдем скорость точки 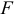как вращательную 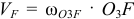, откуда

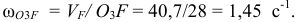
Угловую скорость 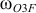изображаем круглой стрелкой вокруг точки 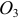, направляя ее в соответствии с найденным уже направлением вектора .

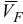Графическое определение ускорений всех точек и угловых ускорений всех звеньев механизма

Для графического определения ускорений точек вычерчиваем схему механизма для заданного положения в масштабе 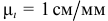(рис. 2.11).

Выбираем масштаб ускорений согласно известным по модулю 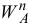и .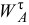

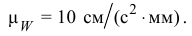
Графически определяем ускорение точки 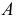по формуле:

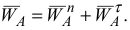
Модули ускорени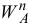й и 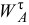известны (п. 2 примера выполнения задачи)

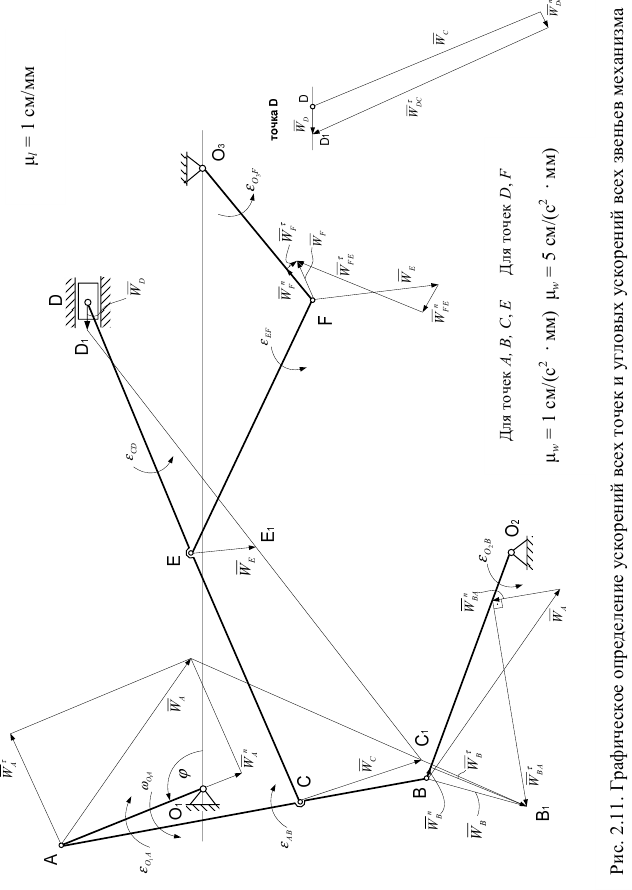
В выбранном масштабе откладываем вектор , направляя его от точки к неподвижной точке и вектор 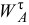, проводя его перпендикулярно вектору 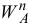(или 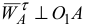) в направлении углового ускорения 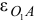звена .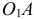

Вектор 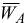найдется как диагональ параллелограмма (в данном случае прямоугольника), построенного на векторах 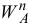и 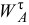как на сторонах.

Модуль ускорения точки 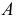найдется через масштаб ускорений

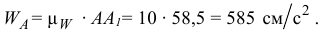
Принимая точку 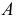за полюс, определим ускорение точки 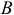при помощи теоремы об ускорениях точек плоской фигуры:

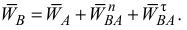
Ускорение точки 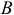можно определить по формуле

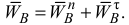
С учетом зависимости (5) выражение (1) принимает вид

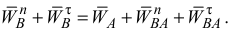
Определим модули тех ускорений выражения (6), которые могут быть вычислены

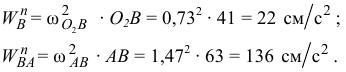
В выбранном масштабе строим многоугольник ускорений согласно зависимости (6). Согласно правой части уравнения (6) от точки откладываем вектор ускорения , из конца которого проводим вектор 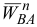, известный по модулю и направленный параллельно звену 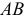к полюсу 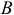. Из конца вектора проводим прямую перпендикулярно звену 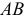, соответствующую направлению вектора 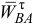, модуль которого неизвестен.

Согласно левой части уравнения (6) из точки 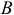откладываем вектор 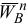, известный по модулю и направленный вдоль 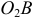к оси 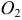. Из его конца проводим прямую перпендикулярно звену 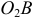, которая соответствует направлению неизвестного по модулю вектора 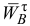, до пересечения с прямой, соответствующей направлению вектора .

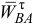Полученную точку пересечения 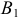соединяем с точкой 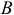. Найденный вектор 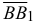геометрически равен вектору 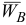, т. е. 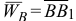. Измеряя его длину 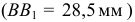и умножая на масштаб ускорений 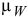, вычисляем модуль ускорения точки :

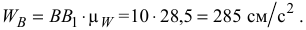
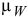Из построенного многоугольника ускорений, измерив длины неизвестных по модулю ускорений и и умножив на масштаб , найдем:

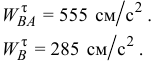
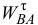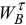Зная, что модули и вычисляются по формулам

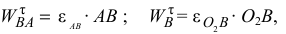
определим угловые ускорения звеньев:

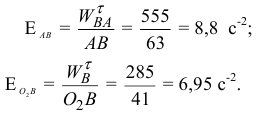
Направление угловых ускорени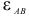й и 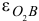в определим по направлению найденных ускорени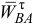й и 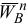соответственно и обозначим круглыми стрелками вокруг звеньев 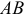и .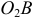

Найдем ускорение точки 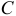, используя известное свойство: концы ускорений точек неизменяемого отрезка лежат на одной прямой и делят её на части, пропорциональные расстояниям между этими точками.

С этой целью соединим концы векторов ускорений точек 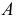и 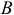отрезком 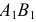. На этом отрезке должен лежать конец вектора ускорения точки 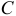. Положение конца вектора ускорения точки 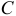на этой прямой определяется из соотношения

Измерив на чертеже отрезок

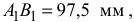
получим:

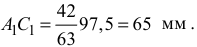
Откладывая от точки 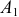отрезок 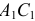и соединяя точку 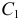с точкой 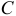, находим 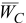— вектор ускорения точки 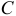. Измеряя его длину 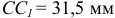и умножая на масштаб ускорений 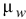, получаем модуль ускорения точки .

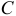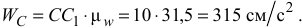
Ускорение точки 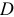найдем аналогично определению ускорения точки 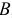, принимая при этом за полюс точку :

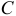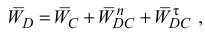
где 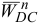— нормальное ускорение точки 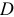во вращательном движении вокруг полюса ;

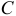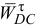— касательное ускорение точки 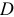во вращательном движении вокруг полюса .

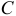Вычислим модуль ускорения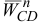

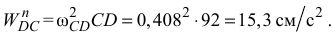
Так как модуль ускорения 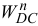значительно меньше модуля ускорения 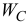, то увеличим масштаб ускорений для точки 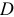до 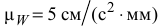. Поэтому, чтобы не загромождать чертеж, в соответствии с векторным равенством (7) строим многоугольник ускорений для точки 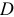в выбранном масштабе вне механизма (рядом с ним).

Поскольку точка 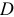движется вдоль горизонтальных направляющих, то ускорение ее направлено по горизонтальной прямой. Проведем эту прямую. Затем от точки 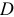откладываем вектор найденного ускорения 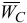в новом масштабе. Из его конца проводим известный по модулю вектор 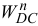параллельно звену 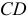, направляя его к полюсу 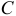. Из конца вектора 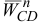проводим прямую перпендикулярно звену 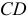, что соответствует направлению неизвестного по модулю ускорения 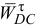. Точка пересечения 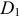этой прямой с горизонтальной прямой, проведенной из точки 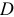, определит вектор 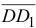, который геометрически равен вектору ускорения 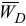. Измерив его, вычислим через масштаб ускорений модуль ускорения точки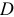

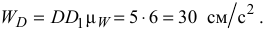
Аналогично, измерив длину вектора 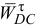, найдем:

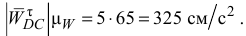
Угловое ускорение звена 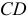найдем по формуле

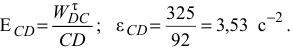
Направление углового ускорения 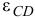определим согласно направлению вектора 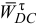и покажем круглой стрелкой вокруг звена .

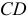Найденный вектор 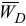в уменьшенном (прежнем) масштабе

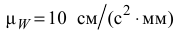
приложим к точке механизма.

Ускорение точки 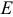звена 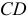найдем по аналогии с определением ускорения точки 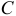, используя свойство ускорений точек, лежащих на одной прямой. Соединим концы векторов ускорений точек 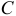и 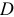отрезком 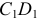. Положение конца вектора ускорения точки 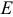найдем из соотношения

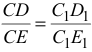
откуда

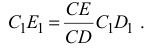
Отрезок 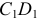измеряем на чертеже 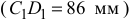и вычисляем

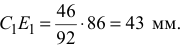
Отложив 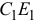от точки 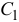и соединив точку 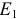с точкой 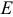, найдем 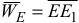. Измеряя отрезок 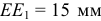, определим:

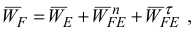
где 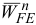— нормальное ускорение точки 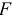во вращательном движении вокруг полюса ,

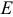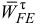— касательное ускорение точки 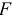во вращательном движении вокруг полюса .

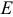Точка 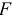также принадлежит звену 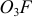, которое вращается вокруг неподвижной оси, проходящей через точку 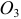. В этом случае ускорение точки 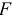определяется по известной формуле

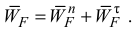
С учетом (9) зависимость (8) примет вид

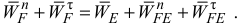
Вычислим модули ускорений, данные для которых имеются

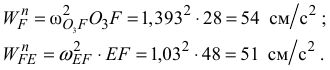
Построим при точке 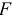в увеличенном масштабе

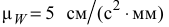
многоугольник ускорений согласно зависимости (10).

Согласно правой части уравнения (10) от точки 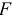механизма отложим вектор ускорения полюса 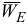в выбранном масштабе. Из конца этого вектора проведем вектор 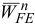параллельно звену 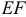, направив его к полюсу а из конца вектора 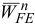перпендикулярно звену 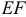проведем прямую, по которой направлен вектор ускорения 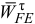. Затем согласно левой части уравнения (10), отложим от точки 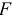известный по модулю вектор ускорения 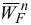, направляя его вдоль звена 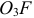к неподвижной точке 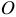. Из конца вектора 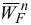проводим прямую перпендикулярно звену 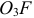, соответствующую направлению вектора 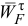до пересечения с ранее проведенной перпендикулярно звену 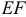прямой. Соединяя полученную точку пересечения этих прямых 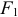с точкой 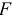, определяем вектор ускорения 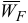точки , т.е. 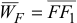. Измерив длину этого вектора , найдем модуль вектора 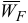через масштаб ускорений:

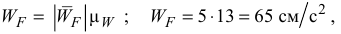
и по аналогии определяется модуль вектора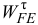

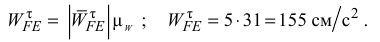
Так как

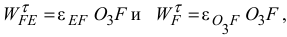
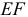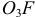то угловые ускорения звеньев и равны

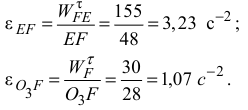
Направление угловых ускорени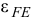й и 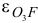обозначим круглыми стрелками вокруг звеньев 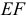и 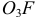в соответствии с направлениями найденных векторов 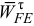и .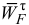

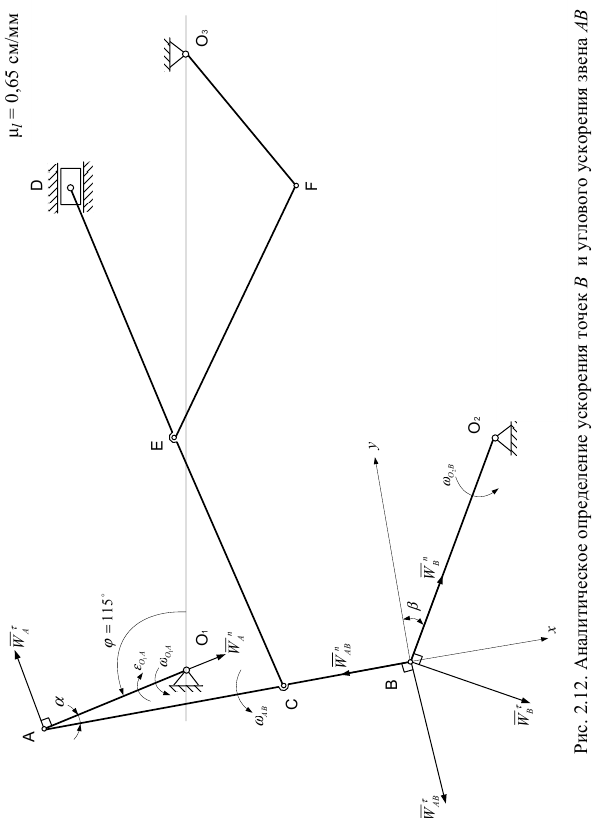
Аналитическое определение ускорения точки 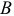и углового ускорения звена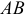

Схема механизма рисуется в выбранном масштабе длин. В данном случае 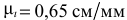(рис. 2.12). Для аналитического определения ускорения точки воспользуемся теоремой об ускорениях точек плоской фигуры.

Принимая за полюс точку , выразим ускорение точки по формуле

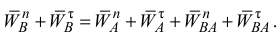
В этом векторном уравнении известны по модулю и направлению ускорения

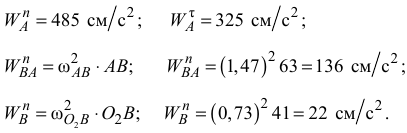
Для ускорени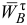й и 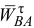известны лишь прямые, по которым они направлены. Надо определить направления этих ускорений и их модули. Согласно векторному равенству (6) из точки 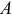без соблюдения масштаба проведем векторы 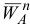вдоль звена , направляя его к точке , и (или 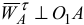) по направлению круглой стрелки углового ускорения 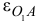звена .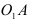

Затем из точки 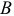, не соблюдая масштаб, проведем вектор 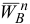вдоль звена 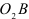, направляя его к точке 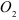, вектор 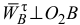, предполагая направленным в произвольную сторону, вектор 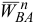вдоль звена 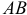, направляя его к точке 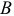, и вектор 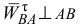, направленным в произвольную сторону.

Выберем систему координат 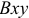с началом в точке 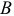и спроектируем векторное равенство (11) на ос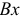и и .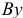

Проектируя равенство (11) на ось 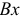, получим:

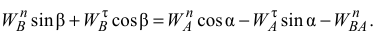
Измеряя углы и 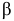непосредственно на чертеже, определяем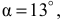 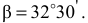Тогда

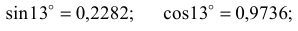
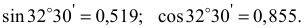
Из уравнения (12) выражаем

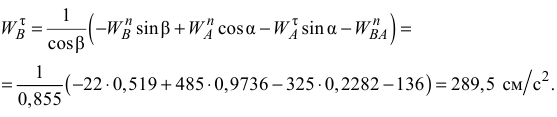
Зная, что

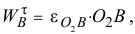
определим угловое ускорение звена :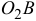

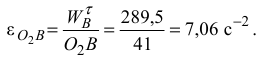
Ускорение точки 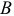найдется по формуле

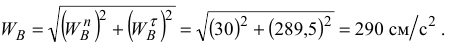
В проекции на ось 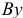векторное равенство (6) запишется

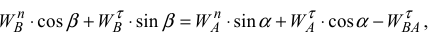
откуда

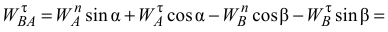
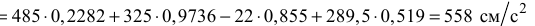
Известно, что

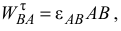
тогда определим угловое ускорение звена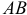

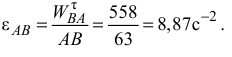
Следует заметить, что если при вычислениях значения ускорени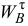й и 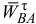получатся отрицательными, то векторы 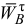и 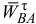в действительности направлены противоположно направлениям, указанным на чертеже.

По аналогии можно аналитически определить ускорения точек 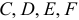и угловые ускорения звеньев 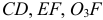данного плоского механизма.

Определение положения мгновенного центра ускорений звена 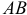и ускорение его средней точки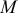

При определении положения мгновенного центра ускорений необходимо начертить схему механизма для заданного положения (рис. 2.13) в выбранном масштабе. В данном случае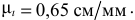

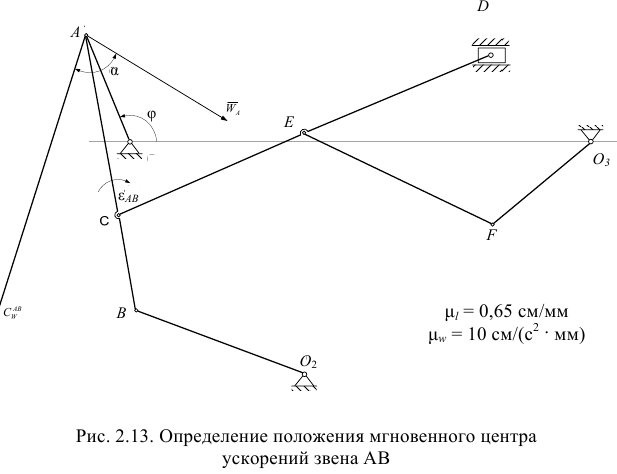
Положение мгновенного центра ускорений определим аналитическим способом. При этом по ранее найденным значениям

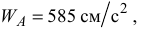
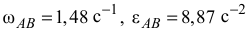
определяем следующие величины:

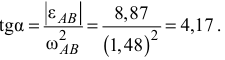
Откуда

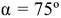
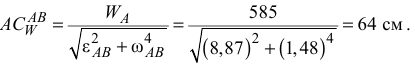
На схеме механизма проводим вектор ускорения 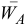в произвольном масштабе. По звену 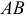показываем круглой стрелкой угловое ускорение .

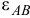Отложим вычисленный угол 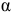от вектора ускорения 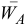в направлении круглой стрелки 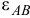и проведем под этим углом отрезок прямой 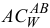в выбранном масштабе длин

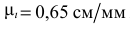
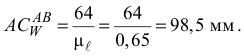
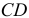Полученная точка является мгновенным центром ускорений звена . По аналогии можно определить положение мгновенных центров ускорений звеньев и .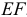

Ускорение средней точки 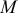звена 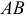определим, зная, что векторы ускорений всех точек звена 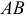образуют одинаковый угол с отрезками, соединяющими точки с мгновенным центром ускорений 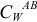этого звена.

Поэтому соединим точку 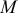с точкой 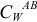. Отложим от прямой 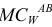угол 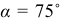в сторону, противоположную круглой стрелке 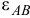, и проведем под этим углом вектор 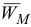ускорения точки .

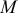Так как модули ускорений точек при плоскопараллельном движении твердого тела пропорциональны соответствующим расстояниям от точек до мгновенного центра ускорений, то модуль ускорения точки 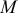найдем, составив пропорцию:

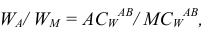
откуда

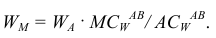
Измеряем отрезк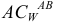и и 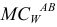на схеме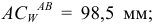

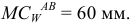
Тогда

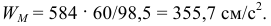
Полученные результаты вычислений по всем пунктам задания сводим в табл. К2 в.

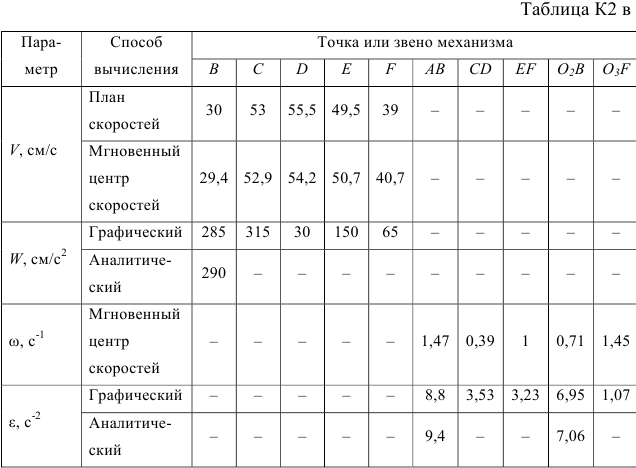
Допускается расхождение между цифрами, полученными различными способами, порядка 3 — 5 %. Образец выполнения чертежей приведен в прил. 5 и 6.