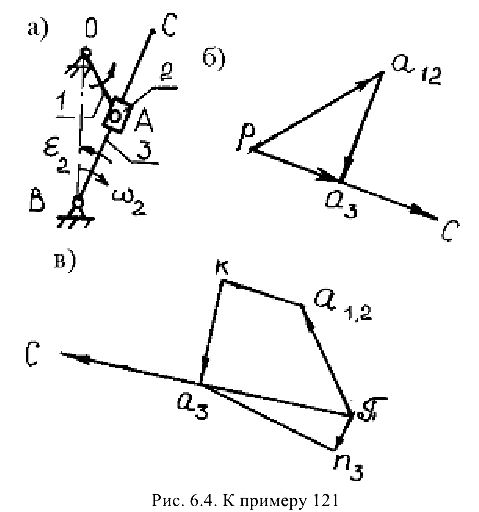
Задача №121. Для механизма Витворта (кулисный механизм, рис. 6.4) построить планы скоростей и ускорений всех звеньев

Задача №121.

Для механизма Витворта (кулисный механизм, рис. 6.4) построить планы скоростей и ускорений всех звеньев, определить линейные скорости и ускорения всех точек, а также угловые скорости и ускорения звеньев. Размеры звеньев:

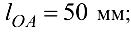
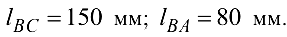
Угловая скорость начального звена 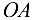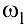постоянна и равна .

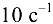Решение:

Формула строения (0, 1) 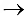> П (2, 3) — механизм второго класса.

Вводим следующие обозначения: 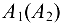— общая точка первого и второго звеньев (центра шарнира); 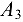— точка, принадлежащая третьему звену и в данный момент совпадающая с точкой .

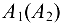Построение плана скоростей. Скорость точки 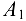начального звена

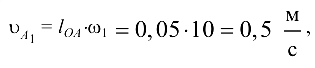
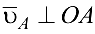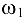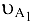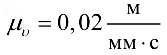причем в сторону . Отрезок, изображающий при равен

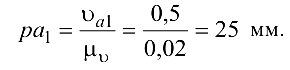
Для определения скорости точки 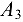рассматриваем движение звена 2 как сложное, которое складывается из переносного движения вместе со звеном 3 и относительного движения по отношению к этому звену. В соответствии с этим составляем векторное уравнение

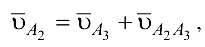
причем

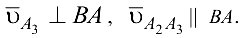
Вместо уравнения (6.11) удобнее использовать равносильное ему уравнение

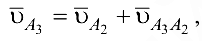
в котором неизвестный вектор 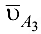находится в левой части. В результате графического решения уравнения (6.12) находим

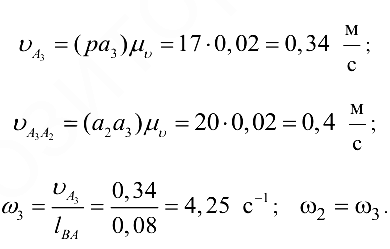
Скорость точки 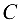определяется на основании теоремы подобия:

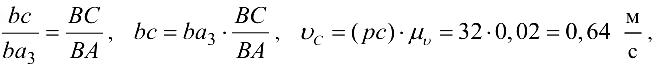
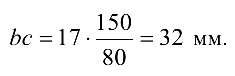
Построение плана ускорении. Так как 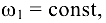то

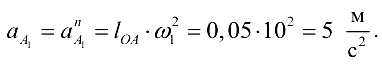
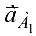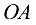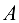Причем вектор направлен вдоль от к 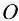. Отрезок, изображающи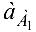й , при

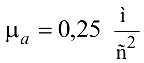
равен

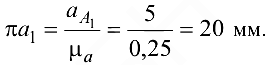
Ускорение точки 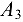находим на основании теоремы о сложении ускорений в сложном движении, известной из теоретической механики:

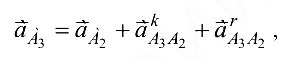
где 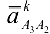— кориолисово ускорение;

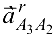— относительное ускорение, причем .

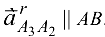В общем случае, как известно,

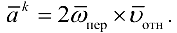
Так как для плоских механизмов

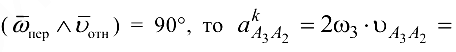
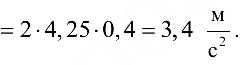
Отрезок, изображающий 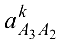, равен

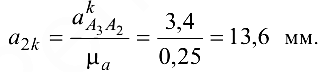
Для определения направления кориолисова ускорения 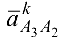используем следующее правило: поворачиваем вектор относительной скорости 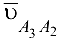(отрезок 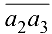) на 90° в сторону переносной угловой скорости .

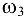Кроме вышеуказанного уравнения (6.13) необходимо использовать следующее уравнение:

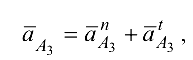
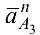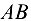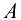в котором вектор нормального ускорения направлен вдоль от к 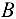, а вектор касательного ускорения 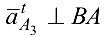. Находим

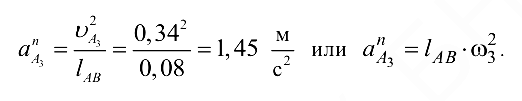
Отрезок, изображающий 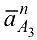, равен

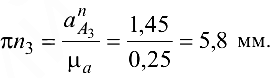
В результате совместного графического решения уравнений (6.13) и (6.14) находим

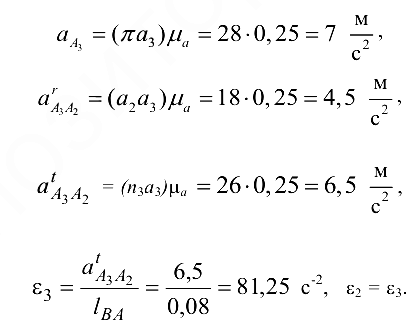
Ускорение точки 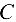определяем на основании теоремы подобия (аналогично скорости точки ):

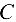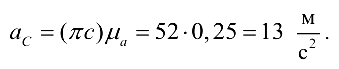
Ответ:

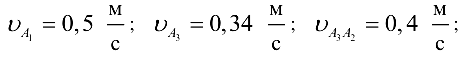
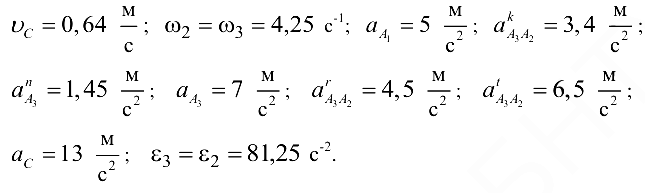
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:

Решение задач по прикладной механике

Возможно эти страницы вам будут полезны:

Задача №119. Определить усилия в стержне пространственной фермы, изображённой на рис. 4.28, а также реакции опор фермы если на узел фермы действуют вертикальная сила = 20 кН и горизонтальная сила =40 кН, направленная вдоль стержня.

Задача №120. Построить планы скоростей и ускорений всех звеньев кривошипно-ползунного механизма (рис. 6.3). Найти линейные скорости и ускорения обозначенных точек и угловые скорости и ускорения звеньев.

Задача №122. Провести кинематический анализ кривошипно-ползунного механизма (рис. 6.5, а): построить 2-3 плана положений механизма, для указанных положений механизма построить план ускорений.

Задача №123. Выполнить кинематический анализ рычажного механизма, представленного на рис. 6.7, а. Построить планы скоростей механизма для двух положений и для одного положения план ускорений.