Пример задачи 5.1
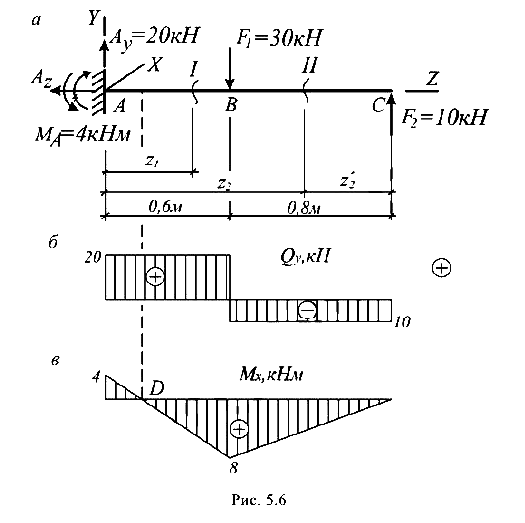
Для консольной балки построить эпюры поперечных сил и изгибающих моментов (рис. 5.6).
Решение
На расчетной схеме балки размещается система координатных осей X, Y,Z с началом в крайнем левом сечении балки.
Действующие на балку нагрузки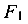 
и 
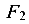передаются на опору (защемление), где возможны три опорные реакци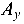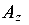и (
, 
и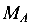 
), которые предварительно направляются произвольно.
Для определения трех опорных реакций используются три уравнения равновесия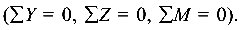 
Значит, рассматриваемая система (балка) является статически определимой.
Рекомендуется следующий порядок определения опорных реакций, пригодный для всех схем балок.
Составляются уравнения моментов относительно крайних сечений балки (здесь точки А и С):
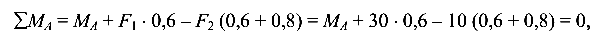
откуда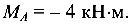 
Знак «минус» при 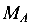указывает на то, что момент направлен в противоположную сторону. На схеме показывается действительное направление 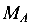, и далее знак «минус» не учитывается.
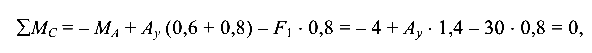
откуда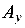 
= 20 кН (направление 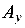правильное).
Из уравнения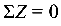 
определяем реакцию :
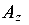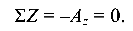
Уравнение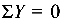 
используется для проверки правильности определения реакций:
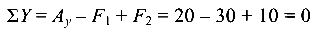— реакции определены верно.
При расположении нагрузки перпендикулярно продольной оси балки реакция опоры вдоль оси Z всегда равна нулю. Поэтому в последующих задачах она не будет указываться.
Для определения Q и М на балке выделяются расчетные участки (здесь — два), в пределах которых помечаются сечения I и II и отмечается их положение в системе координатных осей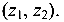 
Составим выражения для определения поперечной силы Q и изгибающего момента М для каждого участка балки.
Участок 1
Рассматриваем левую от сечения часть балки (ход слева):
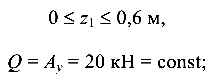
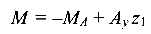— линейная зависимость.
При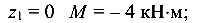 
при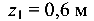 
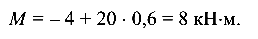
Проверим знаки слагаемых в составленных выражениях.
В выражении для Q реакция 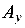дает положительное слагаемое, так как пытается повернуть рассматриваемую часть балки относительно сечения I по ходу часовой стрелки.
В выражении для М опорный момент 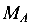дает отрицательное слагаемое, так как стремится изогнуть рассматриваемую часть балки относительно сечения I выпуклостью вверх, а реакция 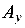положительное значение, так как стремится изогнуть балку выпуклостью вниз.
Участок 2.
Рассматриваем левую от сечения часть балки (ход слева):
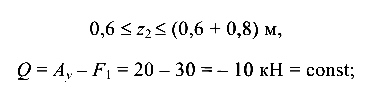
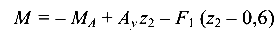— линейная зависимость.
При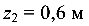 
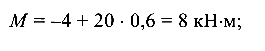
при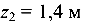 
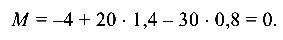
О знаках слагаемых. Сила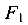 
в выражении для Q дает отрицательное слагаемое, так как стремится повернуть рассматриваемую часть балки относительно сечения II против хода часовой стрелки, а в выражении для М также дает отрицательное слагаемое, так как стремится изогнуть балку выпуклостью вверх.
Заметим, что значения Q и М на концах балки согласуются с действующими здесь нагрузками (реакциями). Так, вычисленное значение Q в сечении С численно равно приложенной здесь силе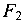 
, а вычисленное значение М численно равно приложенному здесь моменту М (в данном случае М = 0).
Для определения Q и М можно рассматривать и правую часть балки (с началом отсчета ординаты Z в сечении С).
Так, для второго участка (ход справа):
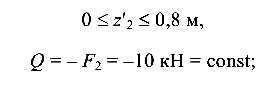
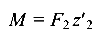— линейная зависимость.
При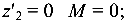 
при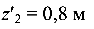 
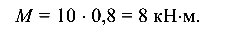
Значения Q и М совпадают с ранее полученными.
Второй вариант составления выражений для Q и М (ход со стороны свободного конца) для консольной балки имеет преимущество в том, что не требуется определения опорных реакций. Но при этом контрольные значения (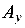,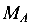) отсутствуют.
По полученным значениям Q и М в характерных сечениях балки в выбранном масштабе строятся эпюра Q (рис. 5.6, б) и эпюра М (рис. 5.6, в). Положительные значения Q откладываются вверх от оси эпюры, а положительные значения М — вниз.
При таком направлении ординат М эпюра изгибающих моментов оказывается построенной со стороны растянутых волокон балки, что удобно в строительном проектировании.
Проанализируем характер эпюр Q и М на участках балки. На участках балки, где нет распределенной нагрузки (q = 0), эпюра Q -прямолинейна, параллельна оси балки, а эпюра М — прямолинейна, наклонна к оси балки.
В сечениях А, В и С, где действуют активные и реактивные сосредоточенные силы, на эпюре Q имеются скачки на величину этих сил.
Если смотреть со стороны крайнего левого сечения балки, то скачки на эпюре Q направлены в сторону действия сосредоточенной силы (активной и реактивной). Так, сила 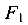направлена вниз -скачок на эпюре Q также вниз, а в сечении С — вверх, так как сила 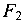направлена вверх.
В сечении балки В, где приложена сосредоточенная сила 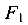, на эпюре М имеется излом.
В сечении балки А, где действует момент 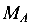, на эпюре М имеется скачок на величину этого момента, направленный вверх, так как 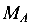направлен против хода часовой стрелки.
Из эпюр Q и М следует, что на участке балки AD верхние волокна растянуты (ординаты М лежат сверху от оси эпюры), а нижние сжаты. На участке DC нижние волокна растянуты, верхние сжаты.
Из построенных эпюр Q и М следует, что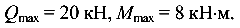
Эти значения нужны для последующих расчетов.
Этот пример решения задачи взят со страницы решения задач с примерами по всем темам предмета «Сопротивление материалов»:
Примеры решения задач по сопротивлению материалов
Дополнительные задачи которые вам будут полезны:
