Задача 1.41.
Для изготовления различных изделий 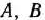 и
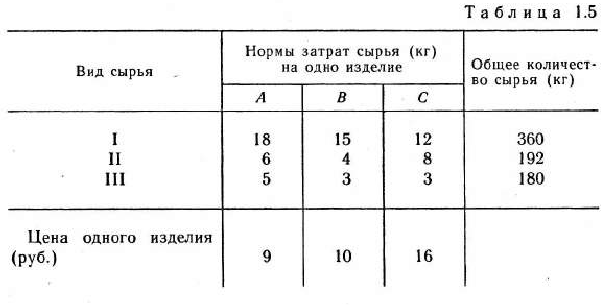
и 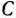 предприятие использует три различных вида сырья. Нормы расхода сырья на производство одного изделия каждого вида, цена одного изделия
предприятие использует три различных вида сырья. Нормы расхода сырья на производство одного изделия каждого вида, цена одного изделия 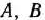 и
и 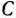 , а также общее количество сырья каждого вида, которое может быть использовано предприятием, приведены в табл. 1.5.
, а также общее количество сырья каждого вида, которое может быть использовано предприятием, приведены в табл. 1.5.
Изделия 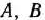 и
и 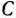 могут производиться в любых соотношениях (сбыт обеспечен), но производство ограничено выделенным предприятию сырьем каждого вида.
могут производиться в любых соотношениях (сбыт обеспечен), но производство ограничено выделенным предприятию сырьем каждого вида.
Составить план производства изделий, при котором общая стоимость всей произведеиной предприятием продукции является максимальной.
Решение:
Составим математическую модель задачи. Искомый выпуск изделий 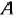 обозначим через
обозначим через 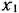 , изделий
, изделий 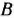 — через
— через 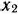 , изделий
, изделий 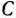 — через
— через 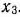 . Поскольку имеются ограничения на выделенный предприятию фонд сырья каждого вида, переменные
. Поскольку имеются ограничения на выделенный предприятию фонд сырья каждого вида, переменные 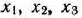 должны удовлетворять следующей системе неравенств:
должны удовлетворять следующей системе неравенств:
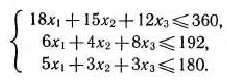
Общая стоимость произведенной предприятием продукции при условии выпуска 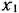 изделий
изделий 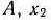 изделий
изделий 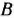 и
и 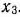 изделий
изделий 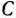 составляет
составляет
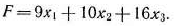
По своему экономическому содержанию переменные 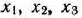 могут принимать только лишь неотрицательные значения:
могут принимать только лишь неотрицательные значения:
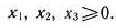
Таким образом, приходим к следующей математической задаче: среди всех неотрицательных решений системы неравенств (29) требуется найти такое, при котором функция (30) принимает максимальное значение.
Запишем эту задачу в форме основной задачи линейного программирования. Для этого перейдем от ограничений-неравенств к ограничениям-равенствам. Введем три дополнительные переменные, в результате чего ограничения запишутся в виде системы уравнений
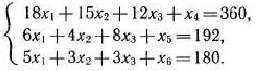
Эти дополнительные переменные по экономическому смыслу означают не используемое при данном плане производства количество сырья того или иного вида. Например, 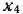 — это неиспользуемое количество сырья I вида.
— это неиспользуемое количество сырья I вида.
Преобразованную систему уравнений запишем в векторной форме:
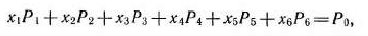
где
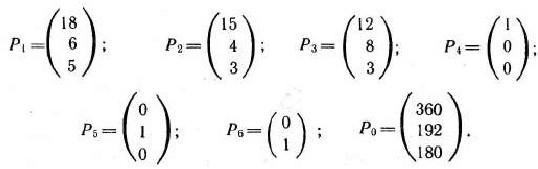
Поскольку среди векторов 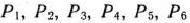 имеются три единичных вектора, для данной задачи можно непосредственно записать опорный план. Таковым является план
имеются три единичных вектора, для данной задачи можно непосредственно записать опорный план. Таковым является план 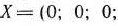
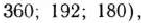 , определяемый системой трехмерных единичных векторов
, определяемый системой трехмерных единичных векторов 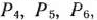 , которые образуют базис трехмерного векторного пространства.
, которые образуют базис трехмерного векторного пространства.
Составляем симплексную таблицу для I итерации (табл. 1.6), подсчитываем значения 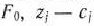 и проверяем исходный опорный план на оптимальность:
и проверяем исходный опорный план на оптимальность:
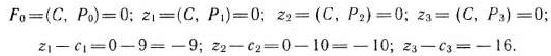
Для векторов базиса
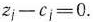
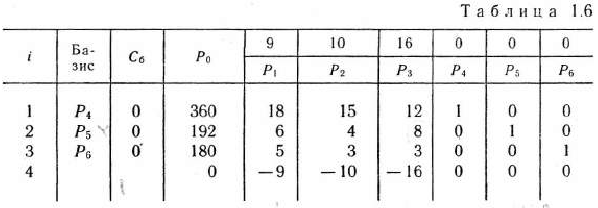
Как видно из табл. 1.6, значения всех основных переменных 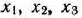 равны нулю, а дополнительные переменные принимают свои значения в соответствии с ограничениями задачи. Эти значения переменных отвечают такому «плану», при котором ничего не производится, сырье не используется и значение целевой функции равно нулю (т. е. стоимость произведенной продукции отсутствует). Этот план, конечно, не является оптимальным.
равны нулю, а дополнительные переменные принимают свои значения в соответствии с ограничениями задачи. Эти значения переменных отвечают такому «плану», при котором ничего не производится, сырье не используется и значение целевой функции равно нулю (т. е. стоимость произведенной продукции отсутствует). Этот план, конечно, не является оптимальным.
Это видно и из 4-й строки табл. 1.6, так как в ней имеется три отрицательных числа; 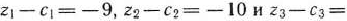
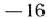 . Отрицательные числа не только свидетельствуют о возможности увеличения общей стоимости производимой продукции, но и показывают, на сколько увеличится эта сумма при введении в план единицы того или другого вида продукции.
. Отрицательные числа не только свидетельствуют о возможности увеличения общей стоимости производимой продукции, но и показывают, на сколько увеличится эта сумма при введении в план единицы того или другого вида продукции.
Так, число —9 означает, что при включении в план производства одного изделия 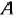 обеспечивается увеличение выпуска продукции на 9 руб. Если включить в план производства по одному изделию
обеспечивается увеличение выпуска продукции на 9 руб. Если включить в план производства по одному изделию 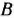 и
и 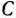 , то общая стоимость изготовляемой продукции возрастет соответственно на 10 и 16 руб. Поэтому с экономической точки зрения наиболее целесообразным является включение в план производства изделий
, то общая стоимость изготовляемой продукции возрастет соответственно на 10 и 16 руб. Поэтому с экономической точки зрения наиболее целесообразным является включение в план производства изделий 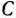 . Это же необходимо сделать и на основании формального признака симплексного метода, поскольку максимальное по абсолютной величине отрицательное число
. Это же необходимо сделать и на основании формального признака симплексного метода, поскольку максимальное по абсолютной величине отрицательное число 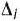 стоит в 4-й строке столбца вектора
стоит в 4-й строке столбца вектора 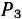 . Следовательно, в базис введем вектор
. Следовательно, в базис введем вектор 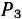 . Определяем вектор, подлежащий исключению из базиса. Для этого находим
. Определяем вектор, подлежащий исключению из базиса. Для этого находим 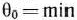
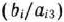 для
для 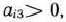 т. е.
т. е.
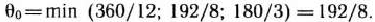
Найдя число 192/8=24, мы тем самым с экономической точки зрения определили, какое количество изделий 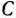 предприятие может изготовлять с учетом норм расхода и имеющихся объемов сырья каждого вида. Так как сырья данного вида соответственно имеется 360, 192 и 180 кг, а на одно изделие
предприятие может изготовлять с учетом норм расхода и имеющихся объемов сырья каждого вида. Так как сырья данного вида соответственно имеется 360, 192 и 180 кг, а на одно изделие 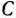 требуется затратить сырья каждого вида соответственно 12, 8 и 3 кг, то максимальное число изделии
требуется затратить сырья каждого вида соответственно 12, 8 и 3 кг, то максимальное число изделии 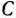 , которое может быть изготовлено предприятием, равно
, которое может быть изготовлено предприятием, равно
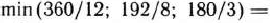
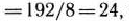
т. е. ограничивающим фактором для производства изделий 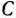 является имеющийся объем сырья II вида. С учетом его наличия предприятие может изготовить 24 изделия
является имеющийся объем сырья II вида. С учетом его наличия предприятие может изготовить 24 изделия 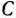 . При этом сырье II вида будет полностью использовано.
. При этом сырье II вида будет полностью использовано.
Следовательно, вектор 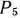 подлежит исключению из базиса. Столбец вектора
подлежит исключению из базиса. Столбец вектора 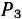 и 2-я строка являются направляющими. Составляем таблицу для II итерации (табл. 1.7).
и 2-я строка являются направляющими. Составляем таблицу для II итерации (табл. 1.7).
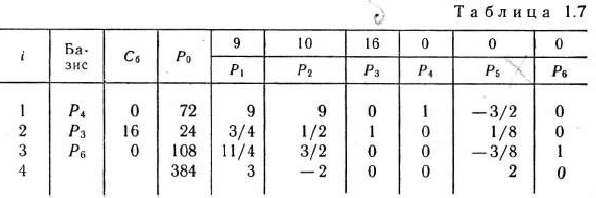
Сначала заполняем строку вектора, вновь введенного в базис, т. е. строку, номер которой совпадает с номером направляющей строки. Здесь направляющей является 2-я строка. Элементы этой строки табл. 1.7 получаются из соответствующих элементов табл. 1.6 делением их на разрешающий элемент (т. е. на 8). При этом в столбце 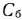 записываем коэффициент
записываем коэффициент 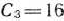 , стоящий в столбце вводимого в базис-вектора
, стоящий в столбце вводимого в базис-вектора 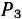 . Затем заполняем элементы столбцов для векторов, входящих в новый базис. В этих столбцах на пересечении строк и столбцов одноименных векторов проставляем единицы, а все остальные элементы полагаем равными нулю.
. Затем заполняем элементы столбцов для векторов, входящих в новый базис. В этих столбцах на пересечении строк и столбцов одноименных векторов проставляем единицы, а все остальные элементы полагаем равными нулю.
Для определения остальных элементов табл. 1.7 применяем правило треугольника. Эти элементы могут быть вычислены и непосредственно по рекуррентным формулам.
Вычислим элементы табл. 1.7, стоящие в столбце вектора 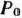 . Первый из них находится в 1-й строке этого столбца. Для его вычисления находим три числа:
. Первый из них находится в 1-й строке этого столбца. Для его вычисления находим три числа:
1) число, стоящее в табл. 1.6 на пересечении столбца вектора 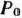 и 1-й строки (360);
и 1-й строки (360);
2) число, стоящее в табл. 1.6 на пересечении столбца вектора 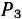 и 1-й строки (12);
и 1-й строки (12);
3) число, стоящее в табл. 1.7 на пересечении столбца вектора 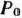 и 2-й строки (24).
и 2-й строки (24).
Вычитая из первого числа произведение двух других, находим искомый элемент: 360—12-24=72; записываем его в 1-й строке столбца вектора 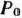 табл. 1.7.
табл. 1.7.
Второй элемент столбца вектора 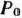 табл. 1.7 был уже вычислен ранее. Для вычисления третьего элемента столбца вектора
табл. 1.7 был уже вычислен ранее. Для вычисления третьего элемента столбца вектора 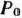 также находим три числа. Первое из них (180) находится на пересечении 3-й строки и столбца вектора
также находим три числа. Первое из них (180) находится на пересечении 3-й строки и столбца вектора 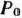 табл. 1.6, второе (3) — на пересечении 3-й строки и столбца вектора
табл. 1.6, второе (3) — на пересечении 3-й строки и столбца вектора 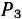 табл. 1.6, третье (24) —на пересечении 2-й строки и столбца вектора
табл. 1.6, третье (24) —на пересечении 2-й строки и столбца вектора 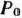 табл. 1.8, Итак, указанный элемент есть 180-24-3=108. Число 108 записываем в 3-й строке столбца вектора
табл. 1.8, Итак, указанный элемент есть 180-24-3=108. Число 108 записываем в 3-й строке столбца вектора 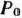 табл. 1.7.
табл. 1.7.
Значение 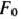 в 4-й строке столбца этого же вектора можно найти двумя способами:
в 4-й строке столбца этого же вектора можно найти двумя способами:
1) по формуле 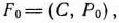 т. е.
т. е. 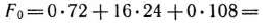
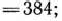
2) по правилу треугольника; в данном случае треугольник образован числами 0, —16, 24. Этот способ приводит к тому же результату: 0— ( — 16) >24 = 384.
При определении по правилу треугольника элементов столбца вектора 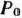 третье число, стоящее в нижней вершине треугольника, все время оставалось неизменным и менялись лишь первые два числа. Учтем это при нахождении элементов столбца вектора
третье число, стоящее в нижней вершине треугольника, все время оставалось неизменным и менялись лишь первые два числа. Учтем это при нахождении элементов столбца вектора 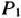 табл. 1.7. Для вычисления указанных элементов первые два числа берем из столбцов векторов
табл. 1.7. Для вычисления указанных элементов первые два числа берем из столбцов векторов 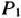 и
и 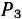 табл. 1.6, а третье число — из табл. 1.7. Это число стоит на пересечении 2-й строки и столбца вектора
табл. 1.6, а третье число — из табл. 1.7. Это число стоит на пересечении 2-й строки и столбца вектора 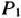 последней таблицы. В результате получаем значения искомых элементов: 18—12 • (3/4) =9; 5-3-(3/4) = 11/4.
последней таблицы. В результате получаем значения искомых элементов: 18—12 • (3/4) =9; 5-3-(3/4) = 11/4.
Число  в 4-й строке столбца вектора
в 4-й строке столбца вектора 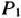 табл. 1.7 можно найти двумя способами:
табл. 1.7 можно найти двумя способами:
1) по формуле
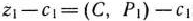
имеем 0-9+16-3/4 + + 0-11/4-9 = 3;
2) по правилу треугольника получим —9 — (— 16)-(3/4) = 3.
Аналогично находим элементы столбца вектора 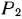 .
.
Элементы столбца вектора 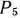 вычисляем по правилу треугольника. Однако построенные для определения этих элементов треугольники выглядят иначе.
вычисляем по правилу треугольника. Однако построенные для определения этих элементов треугольники выглядят иначе.
При вычислении элемента 1-й строки указанного столбца получается треугольник, образованный числами 0,12 и 1/8. Следовательно, искомый элемент равен 0 —12-(1/8) = — 3/2. Элемент, стоящий в 3-й строке данного столбца, равен 0 — 3 • (I /8) = = —3/8.
По окончании расчета всех элементов табл. 1.7 в ней получены новый опорный план и коэффициенты разложения векторов 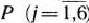 через базисные векторы
через базисные векторы 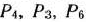 и значения
и значения 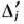 и
и 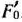 . Как видно из этой таблицы, новым опорным планом задачи является план
. Как видно из этой таблицы, новым опорным планом задачи является план 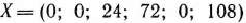 . При данном плане производства изготовляется 24 изделия
. При данном плане производства изготовляется 24 изделия 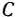 и остается неиспользованным 72 кг сырья I вида и 108 кг сырья III вида. Стоимость всей производимой при этом плане продукции равна 384 руб. Указанные числа записаны в столбце вектора
и остается неиспользованным 72 кг сырья I вида и 108 кг сырья III вида. Стоимость всей производимой при этом плане продукции равна 384 руб. Указанные числа записаны в столбце вектора 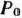 табл. 1.7. Как видно, данные этого столбца по-прежнему представляют собой параметры рассматриваемой задачи, хотя они претерпели значительные изменения. Изменились данные и других столбцов, а их экономическое содержание стало более сложным. Так, например, возьмем данные столбца вектора
табл. 1.7. Как видно, данные этого столбца по-прежнему представляют собой параметры рассматриваемой задачи, хотя они претерпели значительные изменения. Изменились данные и других столбцов, а их экономическое содержание стало более сложным. Так, например, возьмем данные столбца вектора 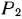 . Число 1/2 во 2-й строке этого столбца показывает, на сколько следует уменьшить изготовление изделий
. Число 1/2 во 2-й строке этого столбца показывает, на сколько следует уменьшить изготовление изделий 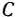 , если запланировать выпуск одного изделия
, если запланировать выпуск одного изделия 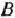 . Числа 9 и 3/2 в 1-й и 3-й строках вектора
. Числа 9 и 3/2 в 1-й и 3-й строках вектора 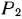 показывают соответственно, сколько потребуется сырья I и II вида при включении в план производства одного изделия
показывают соответственно, сколько потребуется сырья I и II вида при включении в план производства одного изделия 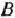 , а число — 2 в 4-й строке показывает, что если будет запланирован выпуск одного изделия В, то это обеспечит увеличение выпуска продукции в стоимостном выражении на 2 руб. Иными словами, если включить в план производства продукции одно изделие
, а число — 2 в 4-й строке показывает, что если будет запланирован выпуск одного изделия В, то это обеспечит увеличение выпуска продукции в стоимостном выражении на 2 руб. Иными словами, если включить в план производства продукции одно изделие 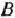 , то это потребует уменьшения выпуска изделия
, то это потребует уменьшения выпуска изделия 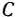 на 1 /2 ед. и потребует дополнительных затрат 9 кг сырья I вида и 3/2 кг сырья III вида, а общая стоимость изготовляемой продукции в соответствии с новым оптимальным планом возрастет на 2 руб. Таким образом, числа 9 и 3/2 выступают как бы новыми «нормами» затрат сырья I и III вида на изготовление одного изделия
на 1 /2 ед. и потребует дополнительных затрат 9 кг сырья I вида и 3/2 кг сырья III вида, а общая стоимость изготовляемой продукции в соответствии с новым оптимальным планом возрастет на 2 руб. Таким образом, числа 9 и 3/2 выступают как бы новыми «нормами» затрат сырья I и III вида на изготовление одного изделия 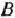 (как видно из табл. 1.6, ранее они были равны 15 и 3), что объясняется уменьшением выпуска изделий
(как видно из табл. 1.6, ранее они были равны 15 и 3), что объясняется уменьшением выпуска изделий 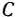 .
.
Такой же экономический смысл имеют и данные столбца вектора 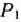 табл. 1.7. Несколько иное экономическое содержание имеют числа, записанные в столбце вектора Число 1 /8 во 2-й строке этого столбца, показывает, что увеличение объемов сырья И вида на 1 кг позволило бы увеличить выпуск изделий
табл. 1.7. Несколько иное экономическое содержание имеют числа, записанные в столбце вектора Число 1 /8 во 2-й строке этого столбца, показывает, что увеличение объемов сырья И вида на 1 кг позволило бы увеличить выпуск изделий 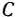 на 1/8 ед. Одновременно потребовалось бы дополнительно 3/2 кг сырья I вида и 3/8 кг сырья III вида. Увеличение выпуска изделий
на 1/8 ед. Одновременно потребовалось бы дополнительно 3/2 кг сырья I вида и 3/8 кг сырья III вида. Увеличение выпуска изделий 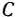 на 1/8 ед, приведет к росту выпуска продукции на 2 руб.
на 1/8 ед, приведет к росту выпуска продукции на 2 руб.
Из изложенного выше экономического содержания данных табл. 1.7 следует, что найденный на 11 итерации план задачи не является оптимальным. Это видно и из 4-й строки табл. 1.7, поскольку в столбце вектора 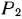 этой строки стоит отрицательное число —2. Значит, в базис следует ввести вектор
этой строки стоит отрицательное число —2. Значит, в базис следует ввести вектор 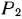 , т. е. в новом плане следует предусмотреть выпуск изделий
, т. е. в новом плане следует предусмотреть выпуск изделий 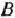 . При определении возможного числа изготовления изделий
. При определении возможного числа изготовления изделий 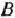 следует учитывать имеющееся количество сырья каждого вида, а именно: возможный выпуск изделий
следует учитывать имеющееся количество сырья каждого вида, а именно: возможный выпуск изделий 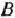 определяется
определяется 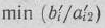 для
для  , т. е. находим
, т. е. находим
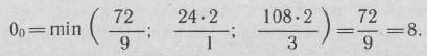
Следовательно, исключению из базиса подлежит вектор 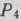 , иными словами, выпуск изделий
, иными словами, выпуск изделий 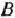 ограничен имеющимся в распоряжении предприятия сырьем I вида. С учетом имеющихся объемов этого сырья предприятию следует изготовить 8 изделий
ограничен имеющимся в распоряжении предприятия сырьем I вида. С учетом имеющихся объемов этого сырья предприятию следует изготовить 8 изделий 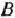 . Число 9 является разрешающим элементом, а столбец вектора
. Число 9 является разрешающим элементом, а столбец вектора 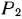 и 1-я строка табл. 1.7 являются направляющими. Составляем таблицу для III итерации (табл. 1.8).
и 1-я строка табл. 1.7 являются направляющими. Составляем таблицу для III итерации (табл. 1.8).
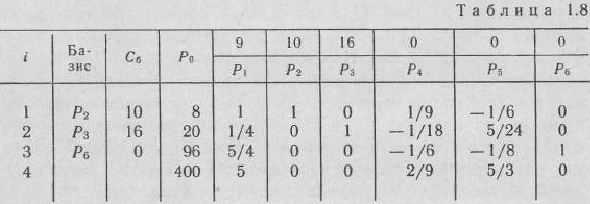
В табл. 1,8 сначала заполняем элементы 1-й строки, которая представляет собой строку вновь вводимого в базис вектора 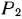 . Элементы этой строки получаем из элементов 1-й строки табл. 1.7 делением последних на разрешающий элемент (т.е. на 9). При этом в столбце
. Элементы этой строки получаем из элементов 1-й строки табл. 1.7 делением последних на разрешающий элемент (т.е. на 9). При этом в столбце 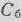 данной строки записываем
данной строки записываем  .
.
Затем заполняем элементы столбцов векторов базиса и по правилу треугольника вычисляем элементы остальных столбцов. В результате в табл. 1.8 получаем новый опорный план
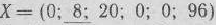
и коэффициенты разложения векторов
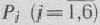
через базисные векторы 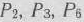 и соответствующие значения
и соответствующие значения 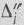 и
и 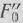 .
.
Проверяем, является ли данный опорный план оптимальным или нет. Для этого рассмотрим 4-ю строку табл. 1.8. В этой строке среди чисел  нет отрицательных. Это означает, что найденный опорный план является оптимальным и
нет отрицательных. Это означает, что найденный опорный план является оптимальным и 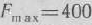 .
.
Следовательно, план выпуска продукции, включающий изготовление 8 изделий 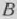 и 20 изделий
и 20 изделий 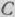 , является оптимальным. При данном плане выпуска изделий полностью используется сырье I и II видов и остается неиспользованным 96 кг сырья III вида, а стоимость производимой продукции равна 400 руб.
, является оптимальным. При данном плане выпуска изделий полностью используется сырье I и II видов и остается неиспользованным 96 кг сырья III вида, а стоимость производимой продукции равна 400 руб.
Оптимальным планом производства продукции не предусматривается изготовление изделии 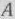 . Введение в план выпуска продукции изделий вида
. Введение в план выпуска продукции изделий вида 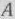 привело бы к уменьшению указанной общей стоимости. Это видно из 4-й строки столбца вектора
привело бы к уменьшению указанной общей стоимости. Это видно из 4-й строки столбца вектора 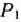 , где число 5 показывает, что при данном плане включение в него выпуска единицы изделия
, где число 5 показывает, что при данном плане включение в него выпуска единицы изделия 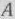 приводит лишь к уменьшению общей величины стоимости на 5 руб.
приводит лишь к уменьшению общей величины стоимости на 5 руб.
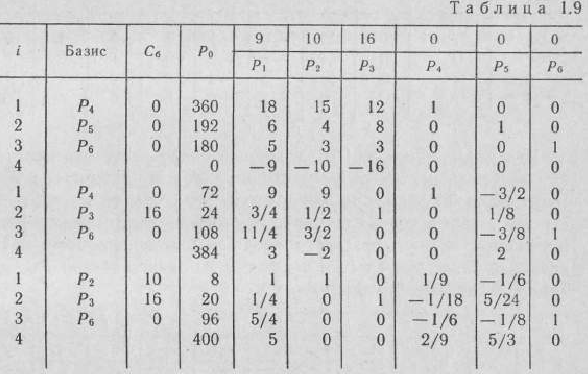
Решение данного примера симплексным методом можно было бы проводить, используя лишь одну таблицу (табл. 1.9). В этой таблице последовательно записаны одна за другой все три итерации вычислительного процесса.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:

