Пример №18.
Для изготовления изделий 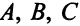 требуется сырье трех видов (I, II, III). Запасы сырья составляют 360, 192, 180 единиц соответственно. Для изготовления одного изделия
требуется сырье трех видов (I, II, III). Запасы сырья составляют 360, 192, 180 единиц соответственно. Для изготовления одного изделия 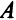 требуется 18 ед. сырья 1,6 ед. сырья И, 5 ед. сырья III. На одно изделие
требуется 18 ед. сырья 1,6 ед. сырья И, 5 ед. сырья III. На одно изделие 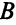 затрачивается 15 ед. сырья I, 4 ед. сырья II, 3 ед. сырья III.
затрачивается 15 ед. сырья I, 4 ед. сырья II, 3 ед. сырья III.
Затраты сырья на изделие 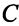 : 12 ед. сырья I, 8 ед. сырья II, 3 ед. сырья III.
: 12 ед. сырья I, 8 ед. сырья II, 3 ед. сырья III.
Стоимость изделий — 9, 10, 16 денежных единиц соответственно. Требуется максимизировать выпуск изделий 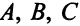 в стоимостном выражении.
в стоимостном выражении.
Математическая модель данной задачи такова:
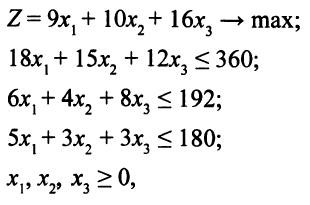
где 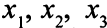 — неизвестные, обозначающие количество изделий
— неизвестные, обозначающие количество изделий 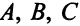 .
.
Построим каноническую модель.
Решим данную ЗЛП симплекс-методом. Покажем только первую и последнюю симплекс-таблицы (табл. 4.5).
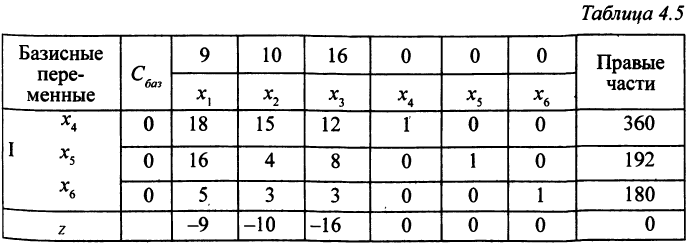
Оптимальное решение: нужно изготовить 8 ед. изделия 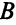 и 20 ед. изделия
и 20 ед. изделия 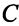 ,
, 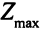 = 400.
= 400.
Если рассматривать переменные 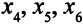 как неиспользованные запасы сырья I, II, III соответственно, то из оптимального решения следует, что запасы сырья I и II полностью израсходованы, а сырья III остается 96 единиц.
как неиспользованные запасы сырья I, II, III соответственно, то из оптимального решения следует, что запасы сырья I и II полностью израсходованы, а сырья III остается 96 единиц.
Выясним, например, в каких пределах может изменяться запас сырья I, чтобы оптимальное решение осталось прежним. Обозначим изменение запаса сырья I через 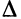 и запишем систему ограничений в виде:
и запишем систему ограничений в виде:
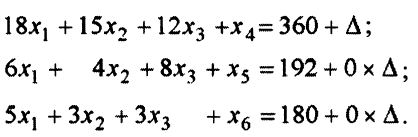
Параметр 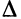 присутствует только в правой части системы ограничений, поэтому при переходе от одной симплекс-таблицы к другой в сравнении с первоначальным вариантом меняться будут только столбцы правых частей. Правые части превратятся в линейные функции от
присутствует только в правой части системы ограничений, поэтому при переходе от одной симплекс-таблицы к другой в сравнении с первоначальным вариантом меняться будут только столбцы правых частей. Правые части превратятся в линейные функции от 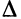 . Коэффициенты
. Коэффициенты 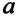 и
и 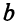 линейной функции
линейной функции 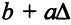 при переходе от одной симплекс-таблицы к другой пересчитываются независимо друг от друга, поэтому столбец правых частей в последней симплекс-таблице примет вид
при переходе от одной симплекс-таблицы к другой пересчитываются независимо друг от друга, поэтому столбец правых частей в последней симплекс-таблице примет вид 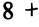
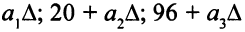 (столбец записан в виде строки).
(столбец записан в виде строки).
Числа 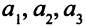 на самом деле известны. Действительно, в первой симплекс-таблице столбец коэффициентов при
на самом деле известны. Действительно, в первой симплекс-таблице столбец коэффициентов при 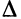 , записанный как строка, таков: (1,0, 0). Он совпадает со столбцом коэффициентов базисной переменной первого уравнения (в данном случае — это переменная
, записанный как строка, таков: (1,0, 0). Он совпадает со столбцом коэффициентов базисной переменной первого уравнения (в данном случае — это переменная 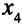 ). Формулы пересчета одинаковы для всех элементов симплекс-таблицы. В любой из них коэффициенты при
). Формулы пересчета одинаковы для всех элементов симплекс-таблицы. В любой из них коэффициенты при 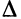 равны соответствующим элементам столбца для переменной
равны соответствующим элементам столбца для переменной 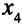 . В частности, в оптимальной для исходной задачи симплекс-таблице
. В частности, в оптимальной для исходной задачи симплекс-таблице
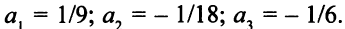
Сам столбец правых частей таков:
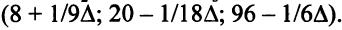
Чтобы найденное решение было оптимальным, достаточна его допустимость (все оценки свободных переменных положительны), т.е. правые части не могут быть меньше 0:
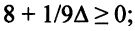
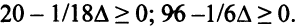
Отсюда:
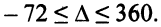
Выясним, что происходит, если меняется один из коэффициентов целевой функции. Пусть, например, коэффициент при 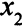 равен 10 +
равен 10 + 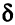 . Для удобства еще раз покажем таблицу с оптимальным решением (табл. 4.6).
. Для удобства еще раз покажем таблицу с оптимальным решением (табл. 4.6).
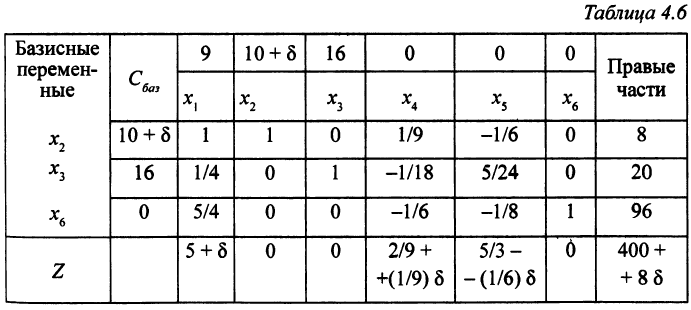
Пересчитаем оценки 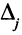 по формуле
по формуле
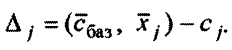
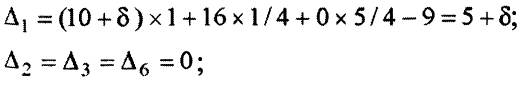
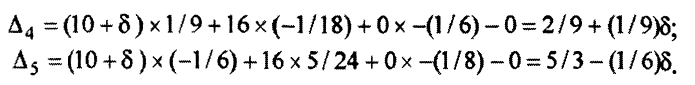
Так как 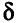 входит только в выражение для
входит только в выражение для 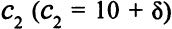 , коэффициенты при
, коэффициенты при 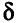 в оценках для свободных переменных и в формуле для
в оценках для свободных переменных и в формуле для 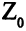 равны соответствующим коэффициентам первой строки (
равны соответствующим коэффициентам первой строки (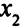 — базисная переменная первого уравнения).
— базисная переменная первого уравнения).
Чтобы найденное решение оставалось оптимальным, все оценки должны быть по-прежнему неотрицательны, то есть должны выполняться неравенства:
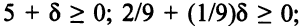
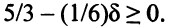
Отсюда
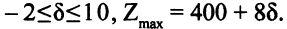
Если разрешить меняться коэффициенту 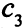 то, учитывая, что в оптимальном решении переменная
то, учитывая, что в оптимальном решении переменная 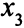 — базисная переменная второго уравнения, получаем такие значения оценок:
— базисная переменная второго уравнения, получаем такие значения оценок:
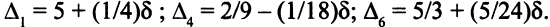
Чтобы все оценки оставались неотрицательными, должны выполняться неравенства:
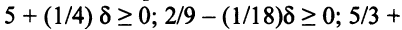
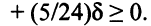
Тогда
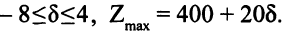
Стоимость 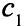 может быть любой, ведь
может быть любой, ведь 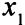 — свободная переменная, в оптимальном решении
— свободная переменная, в оптимальном решении 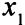 = 0, оценки
= 0, оценки 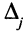 не зависят от значения
не зависят от значения 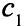 .
.
Выводы, построенные для приведенного примера, легко обобщить.
Далее без комментариев приводится решение ЗЛП, записанное в симплекс-таблицах.
Эта задача взята со страницы решения задач по предмету «линейное программирование»:
Решение задач по линейному программированию
Возможно эти страницы вам будут полезны:

