Задача 1.91.
Для изготовления четырех видов продукции предприятие использует три типа ресурсов. Нормы расхода ресурсов каждого типа на единицу продукции, их наличие в распоряжении предприятия, а также цена единицы продукции приведены в табл. 1.45.
Требуется: а) сформулировать двойственную задачу и найти оптимальные планы прямой и двойственной задач; б) найти
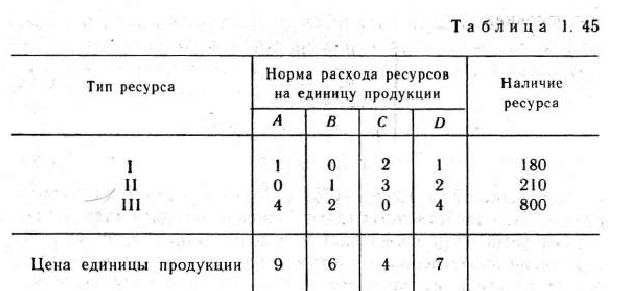
интервалы устойчивости двойственных оценок по отношению к изменениям ресурсов каждого типа; в) выявить изменение общей стоимости изготовляемой продукции, определяемой оптимальным планом ее производства при уменьшении количества ресурса I типа на 60 ед. и увеличении количества ресурсов II и III типов соответственно на 120 и 160 ед. Провести анализ возможного изменения общей стоимости продукции как при изменении объемов каждого из ресурсов по отдельности, так и при их одновременном изменении в указанных размерах.
Решение:
а) Предположим, что изделия видов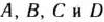 
будут произведены соответственно в количествах 
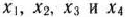. Для определения оптимального плана производства продукции следует найти решение задачи, состоящей в определении максимального значения функции
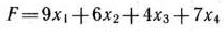
при условиях
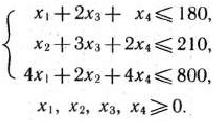
Припишем единице каждого из используемых ресурсов двойственную оценку, соответственно равную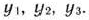 
Тогда двойственная задача по отношению к задаче (73) — (75) состоит в определении минимального значения функции
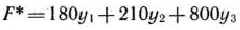
при условиях
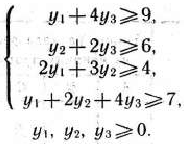
Как видно, задачи (73) — (75) и (76) —(78) образуют симметричную пару двойственных задач. Решение исходной задачи дает оптимальный план производства изделий видов 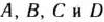, а решение двойственной — оптимальную систему двойственных оценок ресурсов, используемых для производства этих изделий. Чтобы найти решение этих задач, следует сначала отыскать решение какой-нибудь одной из них. Так как система ограничений задачи (73) — (75) содержит лишь неравенства вида 
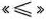, то сначала лучше найти решение этой задачи. Ее решение симплексным методом приведено в табл. 1.46.
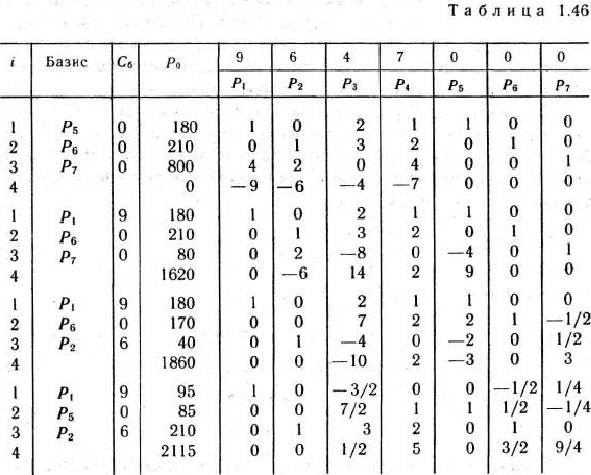
Из этой таблицы видно, что оптимальным планом производства изделий является такой план, при котором изготовляется 95 изделий вида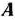 
и 210 изделий вида 
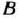. При данном плане производства общая стоимость изделий равна 2115 руб.
Из табл. 1.46 также видно, что оптимальным планом двойственной задачи является
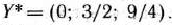
б) Определим теперь интервалы устойчивости двойственных оценок по отношению к изменениям ресурсов каждого вида. Для этого найдем компоненты вектора
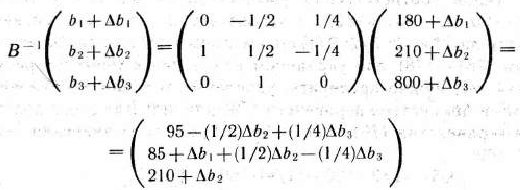
и определим, при каких значениях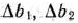 
и 
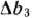они не отрицательны. Прежде чем это сделать, отметим, что матрица 
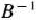обратная матрице 
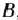, составленной из компонент векторов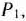 
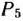и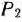 
базиса, который определяет оптимальный план задачи (73)—(75), записана непосредственно на основании данных табл. 1.46, а именно: элементы матрицы 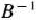взяты из столбцов векторов 
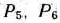и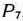 
, образующих первоначальный единичный базис.
Условие неотрицательности компонент указанного выше вектора приводит к следующей системе неравенств:
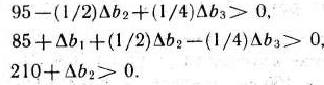
Очевидно, если
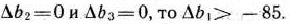
Это означает, что если количество ресурсов I типа будет увеличено или уменьшено в пределах 85 ед., то, несмотря на это, оптимальным планом двойственной задачи (76)—(78) остается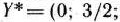 
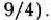
Далее, если
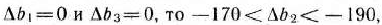
а если
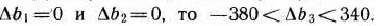
Таким образом, если количество одного из типов ресурсов II или III принадлежит соответственно промежутку
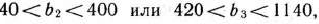
а количество остальных ресурсов остается первоначальным, то двойственная задача (76) — (78) имеет один и тот же оптимальный план
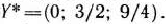
Есл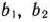и 
и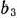 
изменяются одновременно, то исследование устойчивости двойственных оценок несколько усложняется, поскольку в данном случае нужно найти многогранник решений системы линейных неравенств (79). Точки этого многогранника определяют количество ресурсов каждого типа, при которых двойственные оценки остаются прежними.
в) В данной задаче одновременно изменяется количество ресурсов всех трех типов. При этом количество ресурса I типа уменьшается на 60 ед,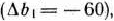 
, а количество ресурсов II и III типов соответственно увеличиваются на 120 и 160 ед. 
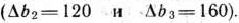. Следовательно, чтобы выяснить, остается ли 
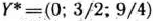оптимальным планом двойственной задачи (76)—(78) при указанном изменении количества ресурсов или нет, нужно проверить, удовлетворяют данные значения 
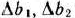и 
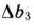системе неравенств (79) или нет. Для этого подставим в неравенства (79) вместо 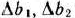и 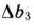их значения —60, 120 и 160:
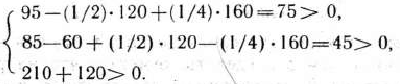
Следовательно, несмотря на изменение объемов ресурсов в указанных размерах, оптимальным планом двойственной задачи останется
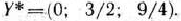
Данное заключение позволяет воспользоваться равенством (72) для определения приращения максимального значения функции (73) при указанных изменениях количества ресурсов. В этом случае
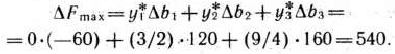
Это означает, что уменьшение количества ресурсов I типа на 60 ед. и увеличение количества ресурсов II и III типов соответственно на 120 и 160 ед. приведет к возможности построения такого плана производства продукции, реализация которого обеспечит выпуск изделий на 540 руб. больше, чем при плане производства продукции, обусловленном первоначальным количеством ресурсов. Уменьшение количества ресурсов I типа на 60 ед. не повлияет на изменение максимального значения функции, в то время как увеличение.количества ресурсов II и III типов на 120 и 160 ед. приведет к увеличению максимального значения функции соответственно на качество сырья L, II и III видов равно 140, 250 и 240 кг.
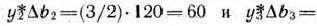
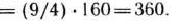
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
