Задача №147.
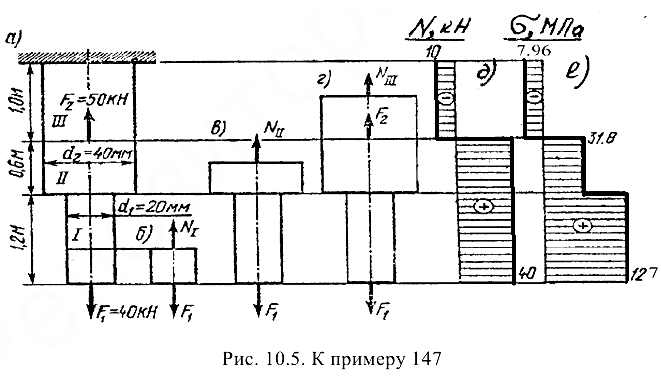
Для двухступенчатого бруса (рис. 10.5) определить и построить эпюры продольных сил и нормальных напряжений. Определить удлинение (укорочение) бруса. Модуль упругости
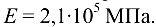
Решение:
Разделим брус на участки, границы которых определяются сечениями, где изменяется площадь поперечного сечения или приложены внешние нагрузки. Мысленно рассечем брус в пределах первого участка и отбросим верхнюю часть бруса (рис. 10.5,б). Сила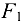 
уравновешивается внутренней силой:
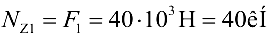
Аналогично в пределах участка II (рис. 10.5, в) отбросим верхнюю часть бруса и рассмотрим оставленную часть бруса с действующей силой 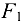, которая уравновешивается продольной силой 
:
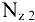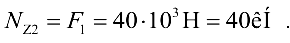
Продольная сила на участке III (рис. 10.5, г) уравновешивается в сечении внешними силам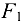и и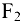 
и равна их алгебраической сумме
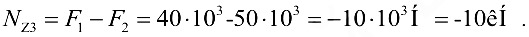
Построим эпюру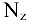 
(рис. 10.5, д). Для этого параллельно оси бруса проведем базовую (нулевую) линию. Левее её откладываем значение продольной силы, вызванной сжатием участка, а правее — растяжением. В пределах участка III брус сжат 
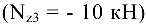, в пределах участков II и I брус растянут 
.
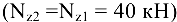Для определения напряжений в поперечных сечениях значение продольных сил необходимо разделить на площади соответствующих сечений.
Площадь поперечного сечения бруса в пределах участка I
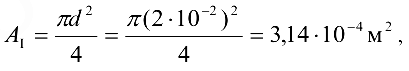
аналогично на участках II и III
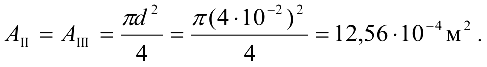
Находим напряжения на отдельных участках бруса и строим эпюру (рис. 2.5, е):
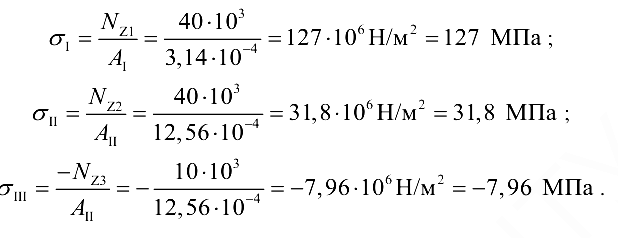
В соответствии с полученными значениями напряжений строим эпюру нормальных напряжений.
Полное удлинение бруса равно алгебраической сумме удлинений его участков:
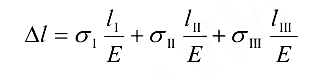
или
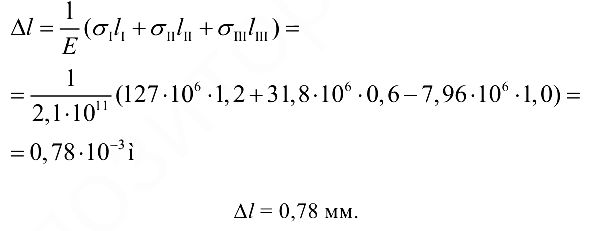
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:
