Оглавление:


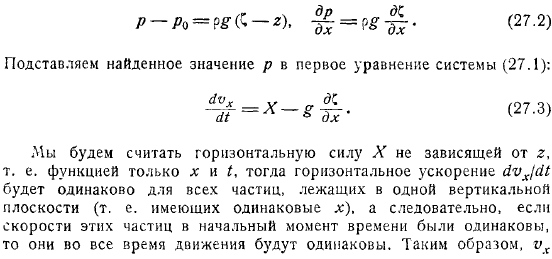



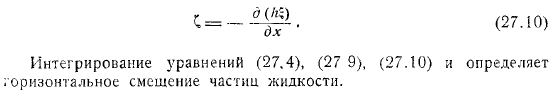

Длинные волны. Основные уравнения
При рассмотрении воли к распространению жидкости конечной глубины выводится уравнение скорости распространения волны c, когда длина волны очень велика по сравнению со следующей. Кроме того, эта скорость не зависит от длины волны. Такие волны называются длинными.
Практическая значимость индивидуального исследования длинных волн заключается в ситуациях. Во-первых, интенсивность независимости скорости распространения волны от длинноволновой длины волны может быть изучена значительно больше, чем в общем случае. Во-вторых, длинные волны — это несколько важных типов волн, таких как приливные волны, которые возникают под действием сил притяжения Луны и солнца.
- Сначала рассмотрим плоскую задачу. То есть предположим, что движение происходит в плоскости, направьте ось вертикально вверх, а ось горизонтально, и получите начало координат свободной поверхности жидкости в положении равновесия.
- Описывается основное уравнение движения для плоского движения несжимаемой жидкости в форме Эйлера.
Он предполагает следующее. Людмила Фирмаль
Вертикальное ускорение частицы ничтожно мало в гидромеханике. То есть, во выражении, это принято. Это означает, что изменение вертикальной скорости частицы происходит очень медленно. За исключением силы тяжести, вертикальная сила может быть.
Другими словами, во выражении. Амплитуда колебаний частиц жидкости очень мала по сравнению с глубиной жидкости. Глубина жидкости в положении равновесия обозначается буквой. В зависимости от расположения, она может быть разной, так как на дне жидкости может не быть.
- Обычно показывают ординату профиля волны, т. е. высоту свободной поверхности жидкости над положением равновесия. Очевидно, что это функция.
- Выражение является. Простота интеграции. Но на свободной поверхности, то есть когда давление должно быть постоянным (атмосферное давление).
Кроме того в прямоугольном сосуде и в круговом цилиндре, в конечном итоге получить следующее. Подставим найденное значение в первое уравнение системы. Горизонтальная сила считается независимой, то есть единственной, и горизонтальное ускорение будет одинаковым для всех частиц в одной вертикальной плоскости (то есть они будут одинаковыми).
Так, если в начальной точке скорости этих частиц одинаковы, то они будут одинаковыми на протяжении всего движения. Людмила Фирмаль
Подобный этому. Только функция. Для этого. Однако по условию и средствам последний термин может быть проигнорирован. Таким образом, уравнение принимает окончательный вид.
Переходим к последнему уравнению. Это и есть уравнение неразрывности. Выведите другое уравнение, которое заменяет это уравнение, и используйте метод, аналогичный тому, который используется для получения уравнения непрерывности.
То есть учитывают объем жидкости, заключенный между неподвижными пространственными вертикальными плоскостями, расположенными перпендикулярно оси (учитывают толщину жидкости в направлении оси, перпендикулярном ОСИ до). Со временем количество жидкости равняется. Здесь значок указывает на абсциссу точки на плоскости.
Через самолет в то же время, количество жидкости в каналах постоянной глубины. Абсцисса точки плоскости. Поэтому количество жидкости между плоскостями уменьшается следующим образом Однако это падение из-за несжимаемости жидкости вызвано только падением уровня жидкости между ними.
Но со временем уровень повышается в среднем, и объем жидкости увеличивается одинаково. Просто уравняйте выражения в одинаковом количестве, с разными знаками, это выглядит так. Но последние члена, которые представляют собой продукт из небольших количеств являются.
Вы получаете окончательное равенство. Итак, длинноволновое уравнение движения в случае планарного движения принимает вид: Вот горизонтальная сила, действующая на единицу массы. Глубина жидкости, высота жидкости над положением равновесия.
Введем горизонтальное смещение частицы из положения равновесия (оно одинаково для всех частиц, находящихся в одном вертикальном положении в первый момент). Очевидно из уравнения. Если вы интегрируете это уравнение, оно выглядит так.
Но любая функция должна быть равна нулю. Потому что если нет горизонтального смещения, то нет и вертикального смещения, то есть того, что есть. Интеграл уравнения определяет горизонтальное перемешивание частиц жидкости.

