Длина дуги плоском кривой
Теорема. Пусть функция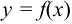 
непрерывна и дифференцируема на 
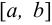и кривая (
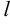) является графиком этой функции. Тогда ее длина на 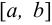вычисляется по формуле:
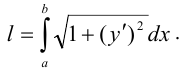
Доказательство. Разобьем отрезок 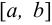точками деления 
, 
.
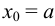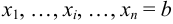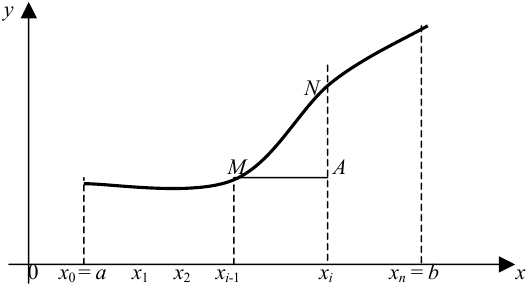
Рассмотрим отрезок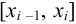 
длины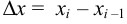 
. На этом участке кривой заменим ее дугу соответствующей хордой. По теореме Пифагора:
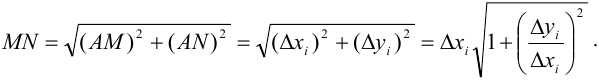
Длиной дуги кривой естественно считать предел суммы всех отрезков ломаной линии, которые заменяют соответствующие дуги кривой по всем точкам деления при условии, что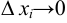 
для всех 
:
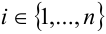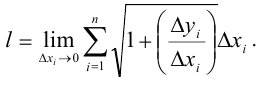
Из построения следует, что указанная сумма является интегральной, а ее предел равен:
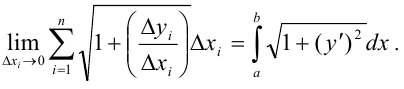
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
| Методы вычисления определённых интегралов задачи с решением |
| Вычисление площадей фигур задача с решением |
| Объем тела вращения в высшей математике |
| Вычисление несобственных интегралов задачи с решением |
