Задача №27.
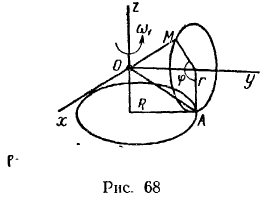
Диск радиуса 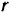 катается без скольжения по плоскости, описывая окружность радиуса
катается без скольжения по плоскости, описывая окружность радиуса 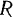 с постоянной по величине угловой скоростью
с постоянной по величине угловой скоростью 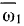 и сохраняя свою плоскость вертикальной. Найти осе стремительное ускорение
и сохраняя свою плоскость вертикальной. Найти осе стремительное ускорение 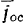 и вращательное ускорение
и вращательное ускорение  точки
точки 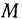 , положение которой на ободе диска определяется углом
, положение которой на ободе диска определяется углом 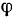 .
.
Решение:
Рассматриваемый диск представляет собой твердое тело с одной неподвижной точкой, так как точка 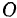 , связанная с телом, остается неподвижной во все время движения.
, связанная с телом, остается неподвижной во все время движения.
Решение задачи можно представить в проекциях на подвижные оси координат 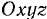 . Линия действия вектора мгновенной угловой скорости о) будет все время проходить через две неподвижные точки
. Линия действия вектора мгновенной угловой скорости о) будет все время проходить через две неподвижные точки 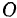 и
и 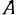 , а потому проекции вектора
, а потому проекции вектора 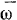 на выбранные оси координат получат вид
на выбранные оси координат получат вид
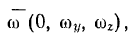
где 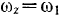 но условиям задачи. Координаты точки
но условиям задачи. Координаты точки 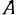 имеют вид
имеют вид 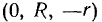 . Определяя теперь скорость точки
. Определяя теперь скорость точки 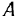 , получим еще одно условие
, получим еще одно условие

откуда найдем

Вектор 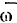 остается постоянным по величине во все время движения. Но конец вектора
остается постоянным по величине во все время движения. Но конец вектора 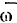 описывает окружность с угловой скоростью
описывает окружность с угловой скоростью 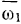 благодаря чему величина вектора
благодаря чему величина вектора 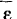 будет равна
будет равна
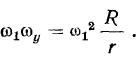
Проекции же вектора 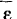 на оси координат получат вид
на оси координат получат вид
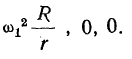
Для определения ускорения точки 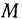 воспользуемся теперь формулой Ривальса:
воспользуемся теперь формулой Ривальса:
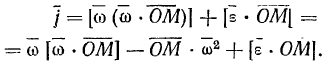
Здесь вектор 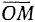 имеет проекции
имеет проекции
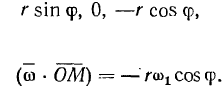
Для проекций ускорения па оси координат получаем следующие значения:
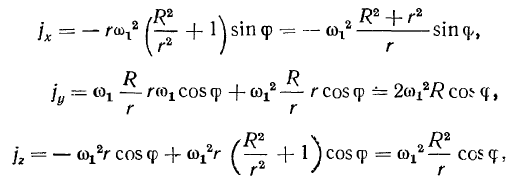
поэтому для полного значения ускорения точки 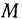 будем иметь
будем иметь
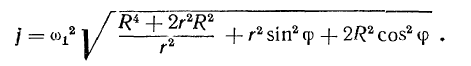
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:

