Дипольное излучение при столкновениях

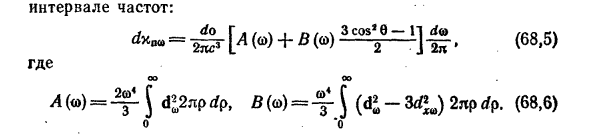
Дипольное излучение при столкновениях

• Дипольное излучение при столкновениях. В радиационных задачах при столкновении (это называется Тормозное излучение) редко является предметом радиации, когда столкновение двух частиц движется по определенной траектории.

Обычно необходимо принимать во внимание рассеяние всего пучка перемещающихся частиц, Задача состоит в том, чтобы определить общее количество излучения на единицу плотности потока частиц.

Единица времени через единицу поперечного сечения частиц пучка проходит через одну частицу Людмила Фирмаль

Если плотность потока частиц в пучке равна 1 (т.е. ), количество частиц в пучке с «расстоянием удара» между p и p + dp составляет 27xpdp (радиус p и p + dp Площадь кольца окружена кружком).

Таким образом, суммарное излучение A S отдельной частицы (путем умножения заданной величины удара получается желаемое суммарное излучение) Расстояние) 27xpdp и интеграл по dp от 0 до os. Количество, определенное таким образом, имеет размер произведения энергии на единицу площади.

• Это называется эффективным излучением и обозначается буквой k). Аналогичным образом, эффективное излучение телесного угла конкретного элемента может быть определено на определенных интервалах частоты duo-n 2). Выведите общую формулу для определения углового распределения Расщепление излучения при рассеянии пучка частиц в центрально-симметричном поле, предполагая, что излучение является диполем.

Интенсивность излучения от каждого момента Отдельная частица определяется по уравнению (67.7). Дипольный момент частицы относительно центра рассеяния 3). Сначала усредните это уравнение по всем направлениям вектора d в ​​плоскости сечения пучка. Поскольку [dn] 2 = d2- (nd) 2, только величина (nd) 2 подлежит усреднению.

из-за центральной симметрии поля рассеяния и параллельности пучка падающих частиц Людмила Фирмаль

Рассеяние (Включая излучение) осесимметричен относительно оси, проходящей через центр. Выберите эту ось Как ось х. Исходя из соображений симметрии, первая степень dy, dz должна быть в среднем равна нулю, а dx Усреднение не влияет йхйу-DXDZ-0.

Поскольку средние значения dy и dz2 равны друг другу, Имея все это в виду, вы можете легко найти [dn] 2 = i (d 2 + dl) + i (d 2-3 dl) cos2 in, Где с — угол между направлением излучения n и осью х. Объединив ход времени и интенсивность всего объема Получите следующее окончательное выражение на расстоянии.

Это определяет эффективное излучение в зависимости от направления. д * ° = Ј? {A + B3-i24 ^ 1) ‘(b8-2) где Герхард Chou A = ^ JJ d2dt27rpdp, B = ^ JJ (d2-For! 2) dt 2npdp. 0-оо 0-оо (68,3) Второе слагаемое в (68.2) записывается так, что полное эффективное излучение усредняется до нуля во всех направлениях, так что k = A j (?.

Угловое распределение излучения Обратите внимание, что луч является симметричным относительно плоскости, которая проходит перпендикулярно лучу — уравнение (68.2) не изменяется, заменяя 0 на 7g-0. Это свойство присуще дипольному излучению и теряется при переходе к более высоким v / c-приближениям.

Интенсивность тормозного излучения Две части: интенсивность излучения, поляризованного в плоскости излучения, проходящей через ось x и направление n (называемой плоскостью xy), и интенсивность излучения, поляризованного в вертикальной плоскости xz.

Вектор электрического поля имеет векторное направление j ^ n [nd] J = n (nd) -d (См. (67.6).) Компонента этого вектора в направлении, перпендикулярном плоскости xy, равна dz и проецируется на плоскость xy. Равен | sin в • dx-cos в • dy | (последний удобнее определять равной z-компонентой магнитного поля в направлении [dn]).

E в квадрате и усредняется по всем направлениям века Для тора d в ​​плоскости yz сначала убедитесь, что произведение проекции поля на плоскость xy и перпендикулярно ей исчезает. Это означает, что интенсивность фактически может быть выражена как сумма двух независимых частей.

Интенсивность излучения поляризована в двух взаимно перпендикулярных плоскостях. Электрический вектор, интенсивность излучения по Перпену Специфично для плоскости xy, определенной средним квадратом Из 4 = i (d 2-4). О соответствующей части эффекта Излучение мы получаем выражение О корка , _L сделать dxn = 4tr <? \ // (^ 2 ~ dl) dt2irpdp. (68,4) Ох ох Обратите внимание, что эта часть излучения изотропна по направлению.

Нет необходимости записывать эффективное уравнение излучения в направлении электрического поля в плоскости xy, поскольку ясно, что: Аналогичным образом можно получить выражение  для уг­лового распределения эффективного  излучения в определенном интервале  частот:

Смотрите также:

• Решение задач по физике

Поле системы зарядов на далеких расстояниях	Тормозное излучение малых частот
Дипольное излучение	Излучение при кулоновом взаимодействии