Динамика твердого тела, вращающегося вокруг неподвижной точки

Динамика твердого тела, вращающегося вокруг неподвижной точки

• Переместить точку, чтобы иметь движение точки движения. 3 степени свободы, чтобы петь, твердое тело, чтобы вращаться. Его позиция определена. Он представлен 3 углами Эйлера. Движение твердого тела относительно основных моментов осей координат, исходных точек, происходит в неподвижной точке. Он задается выражением ЛК х о — Хv ов- Лы 1, ч, —, , р р х о Х 1В, — о- осевой и центробежный моменты инерции твердых тел изменяются при фиксированных осях x, y и z. Если оси x, y и z строго связаны с движущимся гелевым телом, то его ось и центробежный момент инерции постоянны.

Если ось является инерциальной главной осью твердого тела фиксированного типа, если 1гг 1гх 1×1 0, то формула принимает вид Г-Н ПР Где lx, y, 1r-первичный момент инерции твердого тела относительно неподвижной точки. Динамические уравнения Эйлера вокруг неподвижных точек Сплошная проекция па поворот х, г, г Момент лавы внешней силы относительно оси w2 является проекцией угловой скорости твердого тела Координирует Координатные оси. Для x, y и z.

Вектор мгновенной угловой скорости o представлен диагональю параллелограмма, построенного на векторах o и u 9 см. Людмила Фирмаль

С твердым телом связана главная ось инерции в неподвижной точке. Тогда динамическое уравнение Эйлера описывается как А г-4 2л. — Добавьте к этим 3 дифференциальным уравнениям уравнения движения Эйлера, которые представляют зависимость между координатными осями, углами Эйлера и проекциями угловой скорости pa, соответствующими их производным по времени. Sin ФЛ грех п −4 С cos р, ш, , 0 sin косо-б грех МВ Мы получаем 6 систем оды Интегрирование этой системы уравнений арг Начальное условие регулирует вращательное движение твердого тела. Р, ВХ, , ОГА, а также определить уравнение вокруг неподвижной точки 0. 0.

Решение обратной задачи динамики твердого тела, вращающегося вокруг неподвижной точки очень сложно и может быть сведено к квадратуре только в исключительных случаях. Вид обобщенного динамического уравнения Эйлера для движущейся оси etjc, не связанной с твердым телом, имеет вид Решение. Твердые тела движутся по инерции вокруг неподвижной точки o в присутствии внешних сил. O применимо к центру тяжести.

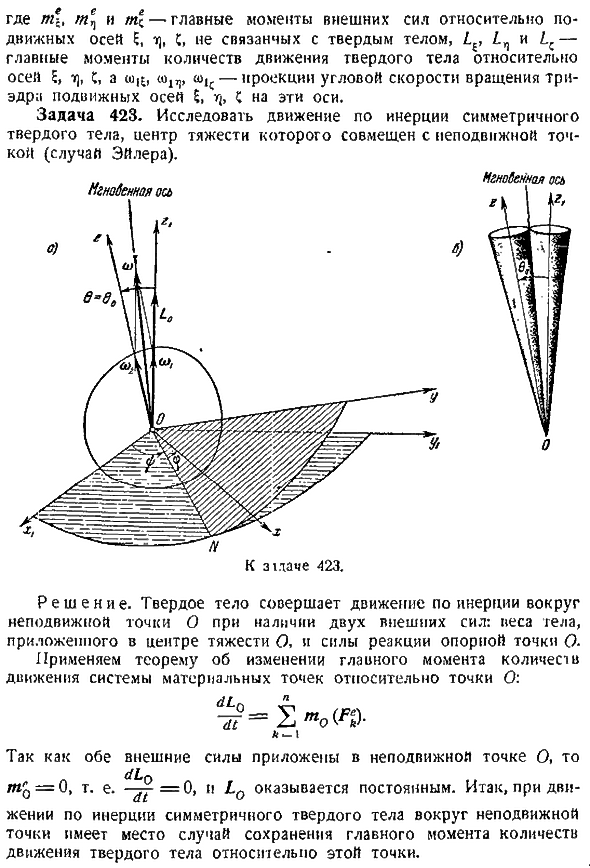
И я поддерживаю эту реакцию. Применить теорему к изменениям в движении материальной системы Обе внешние силы приложены к неподвижной точке o 0, и было обнаружено, что lo constant. So, через день- Из-за инерции окружающего симметричного твердого тела в состоянии покоя Сплошное корпусное движение с сохранением основных моментов объема тела относительно этой точки. Фиксированная ось координат в фиксированной точке o после выбора начала координат системы укажите ось вдоль вектора, направление которого не изменяется при движении твердого тела. Затем укажите фиксированные оси x и yi так, чтобы они образовывали правильную систему координатных осей наряду с осью z.

Начало координат координат x, y и z, связанных с твердым телом, выбирается в той же точке o. Укажите ось z вдоль оси симметрии твердого тела. Далее введем подвижную ось, которая является инерционной главной осью точки oi. Поскольку оси x и y перпендикулярны оси симметрии, 1 1y Запишите динамические и кинематические потери в случае 1×1y и t t А — Г sin 6. Fcosf Формула 1 2 3 Вы можете использовать эту функцию для вычисления интеграла. ОННН. Ive уравнение 1, уравнение 2 pa y, уравнение 3 u r Затем складывание Р -р.

• Ноль 7 Откуда c находится там, где-kg стоит, потому что он вокруг. Энергия вращающегося твердого тела Первый Интеграл 7 подразумевает постоянство кинетической энергии твердого тела этот результат равен нулю, поскольку является суммой работы внешних сил, которую легко получить с помощью теоремы об изменении кинетической энергии материальной точечной системы, так как внешние силы приложены к твердому телу в неподвижной точке. Чтобы определить другие первые интегралы, умножьте уравнение 1 на 1хш уравнение 2 -уравнение 3 -.

Откуда 1xhya x j. Dijot, jibjolj 0, yz m x4 — x o, 8 cs-это константа. Нетрудно заметить, что первый Интеграл, записанный в формуле 8, показывает инвариантность модуля основной величины. O без движения без движения твердых тел. Твердый. Откуда Жюли. Лы ЛР Ай, ЛТ-іх С- -. X, y и r описывают проекцию главного момента momentum. In вид того, что тело, вектор 0, находится на оси r1 см. Рисунок c. После проектирования l на оси крана найдите следующее Л zqsin 6 грех ЛЖ ЛК грех 0cos г, ЛЗ l0cosf.

Система дифференциальных уравнений 3 4 5 6 твердое тело, связанное с движителями x, y, z, чтобы упростить интеграл от 1. Людмила Фирмаль

Используя выражение 9, перепишите выражение 10 в виде 10 А osin0sin 9, ля в п0 грех ocos п р ОГ З. М, потому что 9. 12 13 Из дифференциального уравнения 3 видно, что 2 является постоянной величиной. Мы ведем первый момент, ведут o2o, затем o, w10 при движении. Теперь из уравнения 13 это выглядит так 14 Где lo j l z-5 1-z m является константой. Таким образом, −4 также является постоянной величиной, а угол движения главы равен Во время твердого упражнения остается постоянным.

Оттуда, это продолжается. 0 9 0 0. Здесь выражения 4, 5 и 6 могут быть записаны короче. Sin 0, то sin у, 16 Ай sin9, с cos Р, 17 ДС fc0z90. 18 ty и из Формулы 16 в Формулу 11, а из Формулы 17 в Формулу 12 в. То есть -константа при условии, что она принимает другое значение. Спа-ать Заменять сказал он. ВОДОРОДНЫЙ ПОКАЗАТЕЛЬ 19 20 Г. E. In кроме того, прецессия происходит при постоянной угловой скорости та. Если вы присвоите значение o выражению 18 вместо, то получите Так что f-это константа. После введения обозначения 21 Куда То есть правильное вращение твердого тела происходит с постоянной угловой скоростью w4.

Так, при инерционном движении симметричного твердого тела, где центр тяжести совпадает с неподвижной точкой, происходит упражнение, называемое обычным precession. It объясняется следующим уравнением 0 0,. , 0, p 1 9,. ОСТ. Симметрия трупа z представляет собой круговой лом, равный 0 2О на вершине и вращается равномерно Направление вектора 0, расположенного на оси zt угловой скорости w. In в этом случае твердое тело вращается с угловой скоростью w вокруг оси z симметрии.

Рисунок А и мгновенной угловой скорости В параллелограмме движения твердого тела угловая скорость остается постоянным числом и вращается вокруг оси 2 с постоянной кажущейся угловой скоростью w. Неподвижное осевое тело представляет собой конус, описываемый мгновенной осью вокруг оси z см. Рисунок j. Движущийся Аксон-это конус, который описывается мгновенной осью вокруг оси z.

Смотрите также:

Предмет теоретическая механика

Уравнение Лангранжа второго рода	Регулярная прецессия симметричного твердого тела, имеющего неподвижную точку
Приближенная теория гироскопа	Задачи динамики материальной точки