Оглавление:




















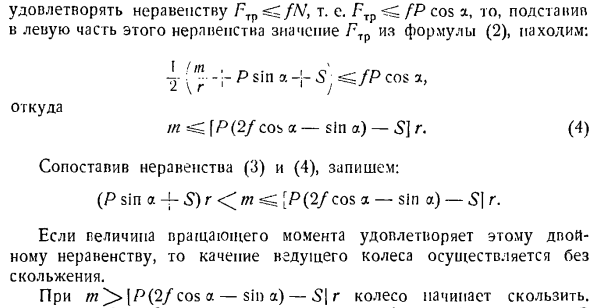









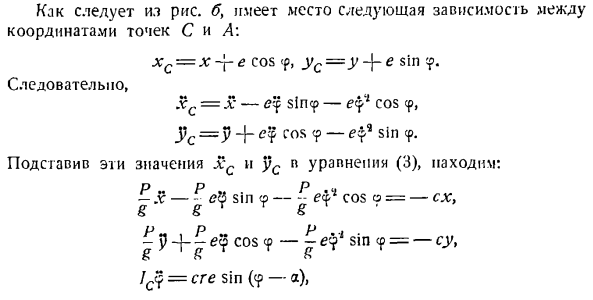






Динамика плоского движения твердого тела
- Динамика плоского движения твердого тела Как известно из кинематики, уравнение плоского движения твердых тел имеет вид ((0.Ус = ((0 -?= ■ = / «(0- Расширяет плоскостное движение твердого тела до поступательного поступательного движения вдоль поступательной оси. Начало координат этой оси лежит в центре инерции твердого тела, а относительное вращательное движение вокруг оси через центр инерции с перпендикулярно неподвижной плоскости (рис.133).Дифференциальные уравнения для плоского движения твердых тел в виде * Сайт mxc = МУС =£Т<, карточка
=£МС(ФГ. ЛТ = 1 Первые 2 уравнения (геолема для движения центра инерции материальной системы, записанные в проекции на оси декартовых координат x и y) описывают поступательное и поступательное движение координатных осей, причем их начало находится в центре инерции твердого тела C. / Я С р р р р * Как и следовало ожидать, для получения
3-е уравнение изменения главного момента импульса системы материи (теорема) имеет движение относительно центра инерции и описывается о случае Людмила Фирмаль
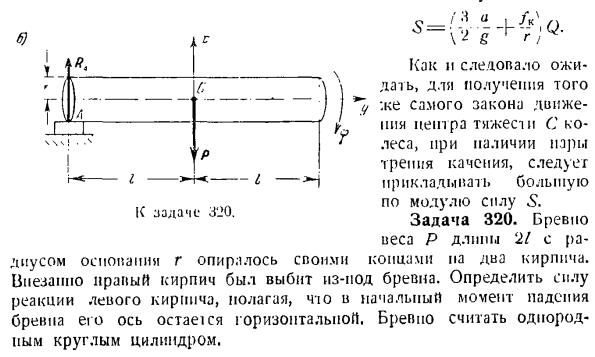
следующего: самого закона движения центра тяжести колеса с, при наличии пары трения качения, следует приложить большую по модулю силу Проблема 320.Логарифм веса длины 2 P / базовый радиус r помещается на концах или 2 кирпичах. Внезапно правый кирпич был выбит из-под земли. log. At в первый момент падения бревна определите силу реакции левого кирпича, предполагая, что его ось остается горизонтальной. Бревно считается однородным
круглым цилиндром. Шесть) Т ’ — Л) В — Л-Х. Задание 320 для 1С. Решение. Если имеется 2 опоры(см. рисунок а), то сила реакции равна П Дой из них такой же, как-у. На рисунке б бревно изображено в первые моменты падения, после чего правый кирпич внезапно снимается. При падении бревно сделает плоское motion. An к бревну прикладывается внешняя сила. Вес журнала P и левая реактивная сила RA кирпича、 Начало координат осей выбирается центроидом
- журнала. оси x и y располагаются на симметричной материалу вертикальной плоскости бревна, направляя ось x вертикально вверх. Создает дифференциальное уравнение для логарифмического плоского движения, которое справедливо для малого угла поворота луча. При составлении 3-го уравнения (I) момент инерции бревна к проходящей горизонтальной оси равен П / р-п \ Его центр тяжести — ^ J Искомая сила реакции входит в правое время первого и третьего уравнений системы(1), левая часть которой равна xc и cf. чтобы исключить xc и§, необходимо найти связь между ними. р»с = ф(а, именно, ХС = — а?(Игнорируйте толщину бревна и предположите, что опора является точечной)、 ЛНР= -/’?(2)) Разрежьте первое уравнени
е (1) системы на 3-е、 / П〜 Получаем выражение(2): — zr= ->>>/» > Л + 4 Реакция левого кирпича: Задача 321.Определите закон движения центра тяжести С колеса автомобиля, поднимающегося в гору, его уклон находится под углом а относительно горизонта. Постоянная сила 5 приложена к оси ведущего колеса, и колесо считается ровным коленом веса А. колеса не скользят и не катятся. Игнорируйте сопротивление качению. Решение. Когда двигатель работает
И это внешняя сила, которая управляет автомобилем. Людмила Фирмаль
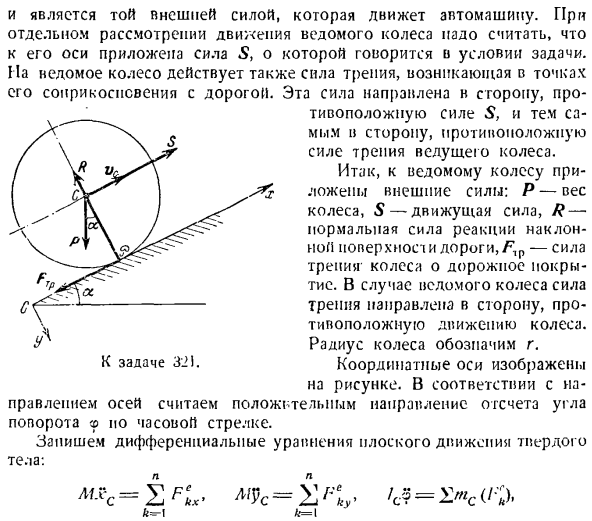
и автомобиль движется, крутящий момент создается на ведущих колесах (обычно на задних колесах).Сила трения, возникающая при соприкосновении ведущих колес с дорожным покрытием, направлена в направлении движения. Рассматривая отдельно движение ведущих колес, следует предположить, что сила S приложена к его оси. Об этом говорится в статусе проблемы. На ведущие колеса также действует
сила трения, возникающая в точке контакта с дорогой. Эта сила направлена в направлении, противоположном силе S, и, следовательно, в направлении, противоположном силе трения ведущих колес. Итак, внешняя сила приложена к ведомому колесу: P-вес колеса, 5-движущая сила, R-сила реакции на наклонную поверхность и дорожную Нормаль,/\, p-сила трения о дорожную поверхность колеса. Для ведущих колес сила трения направлена
в направлении, противоположном движению колес. Радиус колеса Координатные оси показаны на рисунке. Согласно положительному Ось платы считается вращением по часовой стрелке<o. Напишите дифференциальное уравнение для плоского движения твердого тела. Проблема 321. Н. Н. Н. И х ’ Mx ФК-я Форма рассматриваемой задачи выглядит следующим образом: Lxr = С-П грех С Что это? И Г1? = Г г /.
Ноль) Момент трения последнего уравнения системы (1) положителен. Это неудивительно, поскольку его направление совпадает с направлением положительного опорного угла поворота. Когда колеса движутся, yn = — r постоянно, то есть j? Поскольку C = 0, из 2-го уравнения (1)системы мы получаем тот же результат, что и R = P cosa (когда колесо неподвижно) Чтобы определить уравнение движения центроида колеса С, необходимо обобщить первое уравнение системы (1).Тем не менее, правая часть этого уравнения является
Система (I), использующая условие поворота колеса без одновременного скольжения: =(2) (Мгновенный центр скорости колеса находится в точке контакта колеса и дороги).Вычислите производную, но вы получите время og xc: ХС = гхг-(3) Подставив (1) в первое уравнение системы (3) и разделив первое уравнение на 3-е, получим: С-П грех п Откуда / Стеклопластик = PSin а). (4 )) Здесь первое уравнение (I) системы после подстановки значения Fip
из Формулы (4) принимает вид: ХС = — Р грех). Интегрируем это дифференциальное уравнение для начальных условий движения: t = 0, hr = 0, xc-0(по условиям задачи колесо было неподвижным в начальный момент), получаем искомый закон движения центроида C ведущих колес: ХС = ФП (х-р грех) Т \ Если условие 5-Psina ^> 0 выполнено, то есть P sin a, то легко установить, что колесо будет катиться вверх. Часто, решая такие задачи, они ошибочно
полагают, что колеса могут катиться без усилия и без заноса Разногласия. В соответствии с этим предположением, 3-й 。 п Уравнение (1) системы принимает вид r2-f = 0, то есть£= 0. = 0 и я потому что *. (1) (2) г Используйте формулу (3) предыдущей задачи и разделите первое уравнение системы (1) на 3-е уравнение для определения силы трения. П * п = 4 [Р (siluacos в) После подстановки значения Fjp из уравнения(2) первое уравнение системы (1) принимает вид: ХС = [$- п(грех а-j-Г, потому что а)]. 3-е уравнение
Если мы интегрируем последнее дифференциальное уравнение в начальные условия движения£= 0 xc = 0,то найдем закон движения центроида C ведущих колес. ХС = JL и [с-п(грех -] −4 потому что а)] в(3) Из уравнения (3) следует, что условие П ^ синоу-ф ^ ф, потому что а) > 0、 Te. Ы > п [ы \ т \ & + ФФ, потому что ЭйДжей. (4 )) Однако вращение колеса без проскальзывания может происходить с величиной силы, не превышающей определенного предела, соответствующего
предельному значению силы трения / / V. последнее вело Круг приводит к неравенству Fn. Интенсивность нормальной реакции равна L / = P cos a, поэтому^ / P cos a. если вы присвоите уравнению (2) слева от этого неравенства значение f; 1p, то получите: ВТОРОЙ’ / / — П ^ зта-потому что г и J ^ / Pcosa、 Откуда 5 <Р [грех \ 2Ф-потому что Дж. (5) Сравните неравенства (4) и (5) и запишите: / ^ Грех-Джей — ^ коза ^ <5 <П [Шива — | — ^ 2 / — Кост]. (6) Значение S, удовлетворяющее двойному неравенству(6), гарантирует, что ведущие колеса свернутся без slipping. In С> П [грех а-J- [В — Г) потому что] Колеса начинают скользить. Вращение твердого тела вокруг движущейся оси,
движущейся поступательно) представляет собой относительное вращательное движение вокруг оси через центр инерции c твердого тела перпендикулярно неподвижной плоскости. В кинематике любую точку в плане можно считать полюсами, но в механике полюсами следует считать только центр инерции С. Задача 323.При движении автомобиля с уклоном, расположенным под углом а к горизонтали, на ведущие колеса прикладывается пара сил с постоянным крутящим моментом W. Постоянная сила S приложена от ведомой части
транспортного средства к оси c ведущего колеса, которая определяет закон движения центра тяжести c колеса. Колесо считается однородным кольцом массы P и радиуса r. колеса не скользят и не катятся. Не обращайте внимания на трение качения. Решение. 11а действует внешняя сила колеса. P-масса колеса, 5-сила, действующая на ведомую часть транспортного средства, R-
нормальная сила реакции поверхности Земли, пара сил с крутящим моментом t \ FTr-сила трения ведущих колес поверхности Земли-сила движения является движущей силой(для знания колес, рассматриваемых в данной работе). Координатные оси показаны на рисунке. В соответствии с направлением оси, опорное направление угла поворота 9 по часовой стрелке считается положительным. Голы 323
Напишите дифференциальное уравнение для плоского движения твердого тела. м * с =£а, ГГ = £ £ с(0 / Р- = 1 и FC ^ л Принять форму рассматриваемого вопроса = =- / ?- !- Р потому что、 (Приблизительно. ’us = — R является константой, поэтому J? Является C = 0 и из 2-го уравнения системы/?= = / > потому что Разделите первое уравнение (1) системы на 3-е уравнение и используйте соотношение xc =r§.Это отношение относится к условию качения колеса без скольжения «» —
ф ((см. решение предыдущих 2 задач) Т \ п \ грех Г-5 Откуда = — r ^ slna + 5). (2) Подставляя значение f’ip из уравнения (1) справа от первого уравнения (2) системы, получаем: Интеграл этого дифференциального уравнения при начальных условиях движения i = 0, xc = 0, xc-0 выражается формулой Как следует из полученного результата, колесо движется вверх из стационарного состояния, условие — Псина-С> 0、 Иначе говоря м>(п грех а + с) г.(3) Однако вращение ведущего колеса без скольжения происходит только тогда,
когда величина крутящего момента TU не превышает определенных пределов. Действительно, сила трения равна Если мы заполним неравенство Ptp пр «- ‘2(/ <*-}-‘ 2-е уравнение системы принимает вид следующего после подстановки и подстановки результирующего значения F: Г3 ^ = 0 j> потому что c = 0 находится в верхней части диска、 В y ’ • = jrpjpt- Это выражение эквивалентно опусканию диска. Обратите внимание, что ускорение усов не изменяется, независимо
от направления движения центра диска. C-weight. At при крайне низком положении диска происходит удар, скорость центра тяжести С превращается в пулю и меняет свое направление. Задача 325.Масса р и радиус R3 катушки, под действием силы тяжести, соскальзывают и скатываются с наклонной плоскости, расположенной под углом а к горизонтали plane. In в этом случае 2 нити разматываются и наматываются на ось катушки с радиусом rx симметрично относительно вертикальной плоскости симметри
и материала (на рисунке прямая часть нити показана в виде 1 Прямой линии).Когда катушка движется, ее ось остается горизонтальной. C определить силу реакции нити в катушке и скорость движения центра тяжести. p-радиус инерции катушки относительно оси через центроид C, перпендикулярный неподвижной plane. At в первый момент катушка была неподвижна. Коэффициент трения скольжения катушки на намотанной наклонной поверхности. Решение. Внешняя сила приложена к катушке: P вес катушки,
27 полная реактивная сила резьбы, R нормальная реактивная сила наклонной плоскости, Fr? Сила трения катушки скользит по наклонной плоскости. Скатываясь вниз и вращаясь по часовой стрелке, F1 p направляется вверх по наклонной плоскости.
Выберите осям XY, показанной на рисунке. Считаете ли вы, что основное направление угол C будет положительным? По часовой стрелке. Создайте дифференциальные уравнения для плоского движения катушки. = Х-2’/’ -/; Мп、 п США = р-р соз а,£ / П1? = 2 7T1 — / VS-C) Из-за движения катушки Vc = r> 2 ° post и » mo » r-c-X — = O- Из 2-го уравнения (1) системы найти величину вертикальной силы
реакции плоскости. Р = р потому что. (2) Для определения силы реакции нити’/’ необходимо исключить xc из первого и третьего уравнений системы (I). Вам нужно установить зависимости Между ними. Заметим, что мгновенный центр скорости&находится в точке, в которой нити сходятся от оси катушки (см. рисунок), и опишем vc = r | * с = * резюме чч = $ ц0>? = ¥ » .? = Решение задачи динамики плоского движения твердого тела лучше осуществлять в следующ
ем порядке: 1) вся сила, приложенная к твердому телу, показана на рисунке. 2) Выберите систему координат для определения направления положительного опорного угла поворота 3) Создайте дифференциальное уравнение для плоского движения твердого тела(3-е уравнение/ c $ = н = ^ JMC (Fek) момент инерции твердого тела/(и сумма моментов н Все внешние силы: tf(F%) рассчитывается для оси. Перпендикулярно неподвижной плоскости, пройдитесь
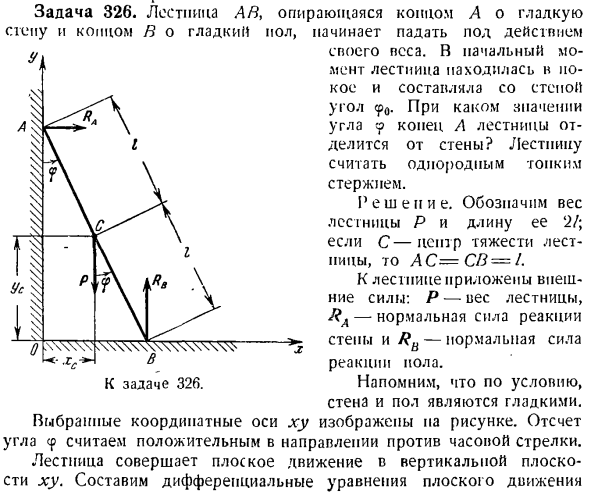
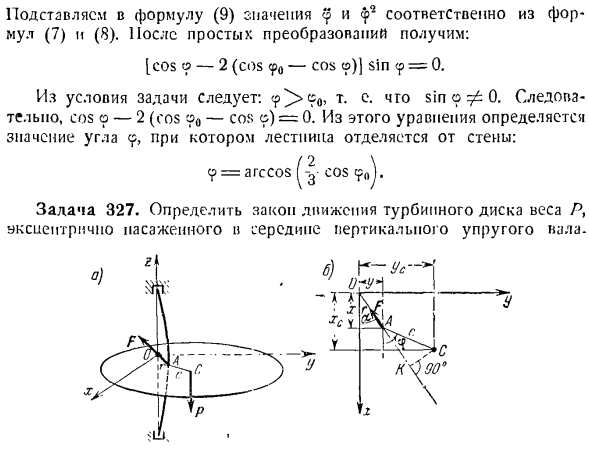
по инерционному центру c твердого тела); 4) а) при решении прямой задачи искомая внешняя сила и ее момент определяются из системы дифференциальных уравнений, составленной в предыдущем пункте. Проблема 326.Лестница поддержанная ровным краем A Stu и ровным краем B. 4/9 пола начинает падать под действием Ваш weight. At на первом этапе лестница была неподвижной и под углом к стене и 0> Й> С = -Р + Rfll(2) Дж / 3? = Р /?/ Грех <П — ^ / cos9. (3) исключить
RA и RB из составленной системы уравнений для представления cp иотносительно o. подставив значение RA в Формулу (1) и значение Rn в Формулу (2) в Формулу (3), результат простого вычисления выглядит следующим образом: Простите? =(ПК » я » и SL «?~ ~ соѕ(4) Как видно из рисунка, jcc = / sin <p, y ^ = I COS 9.Если вы различаете во времени, вы можете увидеть следующее: = / 9 потому что ЛГС = = Щcos 9- / ф9sin 9,(5) АF’с =-/ Ф грех 9, чт-грех 9-/ 9 * потому что 9.(6) Формулы (o) и j (G)?С и J? Подставляя значение C в
Формулу(4) и простое преобразование, получаем формулу от 9 до 9. Три / ? = sincP-в T Чтобы определить зависимость 9 от 9, умножьте дифференциальное уравнение (7) на d <p、9 ^ 9 = ^ </ 9 == 9 </ 9、 Находка: 3 С. 9 <29 = * J В-в прч 9 с / 9. — Ф9 = — г с COS <р с.£= 0 <р = <Р0, если$ = 0.Таким образом, с = | — ycos; Р0.Так… ?9 = .Дж. Ф. (потому что 9o-с COS <Р). (8) (Уравнение (8) можно получить короче, применив теорему к изменению кинетической энергии системы масс, которую мы рассмотрим в следующем разделе.) Теперь можно определить величину угла<p, при котором край лестницы A отделяется от стены. Отделение от ступени РА Он будет равен нулю. И затем…
Значение выражения (9)®ф0. В частности, coso-2(cos £> & си J Р +£*? потому что 9 — £грех СР = Су = СГ £ Sin (с?- ля)、 Откуда Икс-Джей-Син о СУ1 потому что Г -, л и Б » Г = — Е? Потому что? Грех Интегрирование системы дифференциальных уравнений (4) очень сложно. Поэтому она примерно решена. Справа от 3-го уравнения находится произведение эксцентриситета e и sin(9-a).Если мы считаем этот
продукт маленьким, то мы считаем его почти нулевым (небольшая ошибка в этом случае приведена ниже).3-е уравнение (4) системы принимает вид приблизительно<3 = 0.Здесь мы учитываем начальные условия движения. = 0,$ =если найдено: 6 = w и (5) Г. е. вращение диска равномерное. Используйте формулу (o) для описания первых 2 уравнений системы!»! (4) по форме (6) Икс-Джей-КЛК = ч соз(в, г-к * г = ч греха очки Здесь=и Е ^ = сек. Интегралы
дифференциальных уравнений (G) выполняются независимо друг от друга. Общий вид решения этих уравнений выглядит следующим образом: х х-С. потому что т-с. л КТ грех-я — — — Г потому что МАС、 * ’1 л — — -’ ти- Где k = — j / — и U = Как известно, первые 2 члена представляют собой колебания, затухающие при наличии сопротивления, а третий член представляет собой стационарное вынужденное oscillations. So в будущем первые 2 условия будут отброшены. И затем… x = k * — * * cos ^ = s, n (8), то есть точка A
совершает гармонические колебания круговой частоты<o сайт FiiO ’ −1 _ _ И Имлигуды.._ ^.После построения каждого уравнения(/) Когда вы квадрат и сумма, это выглядит так: B, координаты точки A равны x = r cos a, j / = rsina, как следует из рисунка: подставляя значение выражения (8) и значение r в выражение (9) вместо x и y, получаем a = cot. Если сравнить этот результат с выражением(5), то получим: а = <С. (10 )) Если условие a = <p, то точки O, A и C находятся на 1 строке.
(если a = <p, то правая часть 3-го выражения в системе(3)точно равна пуле. Таким образом, погрешность, возникающая при приравнивании правой части 3-го уравнения (-1) системы к пуле, получается путем игнорирования первых 2 членов каждого уравнения системы (7).Учитывая затухание свободных колебаний под действием сопротивления движению, такое приближение следует считать вполне приемлемым. Это хороший пример.) Теперь фото.
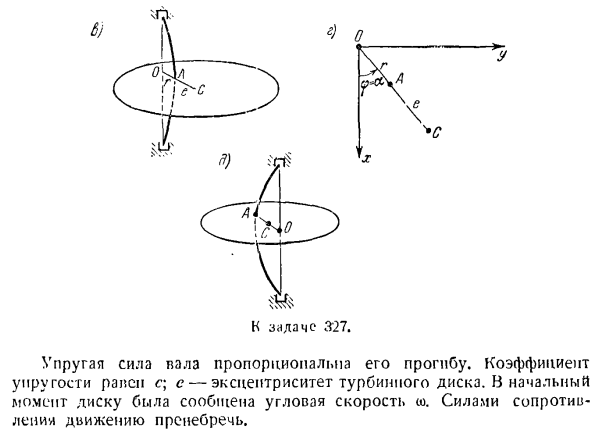
Поскольку точки O, A и C находятся на одной линии, a и b принимают более простую форму (см. Рисунки c и d соответственно). Вычислите смещение центра тяжести диска C от точки O: OS = g + e. By подставляя значение r в выражение (9), можно увидеть: ЕА*, _ ЕК * x1-p_y9 = g9, поэтому прогиб вала равен
продукт маленьким, то мы считаем его почти нулевым (небольшая ошибка в этом случае приведена ниже).3-е уравнение (4) системы принимает вид приблизительно<3 = 0.Здесь мы учитываем начальные условия движения. = 0,$ =если найдено: 6 = w и (5) Г. е. вращение диска равномерное. Используйте формулу (o) для описания первых 2 уравнений системы!»! (4) по форме (6) Икс-Джей-КЛК =
ч соз(в, г-к * г = ч греха очки Здесь=и Е ^ = сек. Интегралы дифференциальных уравнений (G) выполняются независимо друг от друга. Общий вид решения этих уравнений выглядит следующим образом: х х-С. потому что т-с. л КТ грех-я — — — Г потому что МАС、 * ’1 л — — -’ ти- Где k = — j / — и U = Как известно, первые 2 члена представляют собой колебания, затухающие при наличии
сопротивления, а третий член представляет собой стационарное вынужденное oscillations. So в будущем первые 2 условия будут отброшены. И затем… x = k * — * * cos ^ = s, n (8), то есть точка A совершает гармонические колебания круговой частоты<o сайт FiiO ’ −1 _ _ И Имлигуды.._ ^.После построения каждого уравнения(/) Когда вы квадрат и сумма, это выглядит так: B, координаты точки A равны x = r cos a, j / = rsina, как следует из рисунка: подставляя значение выражения (8) и значение r в выражение (9) вместо x и y, получаем a = cot. Если сравнить этот результат с выражением(5), то получим: а = <С. (10 )) Если условие a = <p, то точки O, A и C находятся на 1 строке.
(если a = <p, то правая часть 3-го выражения в системе(3)точно равна пуле. Таким образом, погрешность, возникающая при приравнивании правой части 3-го уравнения (-1) системы к пуле, получается путем игнорирования первых 2 членов каждого уравнения системы (7).Учитывая затухание свободных колебаний под действием сопротивления движению, такое приближение следует считать вполне приемлемым. Это хороший пример.) Теперь фото.
Поскольку точки O, A и C находятся на одной линии, a и b принимают более простую форму (см. Рисунки c и d соответственно). Вычислите смещение центра тяжести диска C от точки O: OS = g + e. By подставляя значение r в выражение (9), можно увидеть: ЕА*, _ ЕК * x1-p_y9 = g9, поэтому прогиб вала равен
Б)а при решении обратной задачи интегрированием системы дифференциальных уравнений движения определяется уравнение плоского движения твердых тел: * с = / Я(0. США = Нет.>??= / а(0- В зависимости от условия задачи можно определить искомую зависимость 2-й координаты от 3-й координаты (например, jcc = F, ( r ^> 0 (см. Рисунки C и d), на основе формул (9) и (11).Для высокочастотных вынужденных колебаний, то есть для co, r ^> | OS | ^> 0, что соответствует изображению на рисунке. д. По мере увеличения диска расстояние OS (см. уравнение (11)) уменьшается
в абсолютном значении. То есть диск, прикрепленный к упругой оси, будет самоцентрированным(m — * oo / OS | — > 0), а его центр тяжести C будет приближаться к геометрической оси брасенипа. Выражение (11)»■= (^ ^ ;. Скорость вращения диска турбины намного быстрее, чем его круговая ОС Собственная частота собственных колебаний, т. е. найденная ОС 1 под Очень малый размер. Например, если вы используете (o:= t>, это будет выглядеть так:= = 0,029.
(Заметим, что в этом случае, когда диск турбины установлен на валу, эксцентриситет е измеряется в микронах.) Явление независимого центрирования фланца на упругом валу было впервые открыто Лавалем в конце 19 века и использовано в конструкции паровой турбины диска, которую он ранее изготовил. 30,000 об / мин / при м «с = iFiv это?= «с (ПУ А-1 * = » ! В этом случае он будет выглядеть так:% * с = с С (1) ■иммуноглобулин Когда колесо движется, yn = — r всегда
будет, то есть pc = 0. Найти уравнение (I) системы: R = Q Если колесо не скользит и не катится, то мгновенный центр скорости находится в точке соприкосновения колеса с горизонтальной плоскостью, поэтому vc =rш. Скорость центра параллельна оси ЛГ.、 И затем… (2) (4 )) «С= Формула (2) определяет вращательное состояние колеса без проскальзывания. Используя формулу (2), рассчитаем: (3) Учитывая движение центра тяжести колеса C, xc = — ^ — t тогда 5пг = а Используйте уравнение 3-го уравнения системы (I) (5) для
определения искомого модуля силы трения. С) Принимая во внимание уравнение (1) из первого уравнения системы (4) и (6), получаем следующее уравнение: Задача 319.Принимая во внимание трение качения колес в горизонтальной плоскости, мы решаем предыдущую задачу. Коэффициент трения качения равен/ к. Из формул(3) и (4) видно, что: Solution. As в результате деформации колеса и плоскости, когда колесо катится по плоскости, их контакт происходит не в 1 точке cT, а на небольшой дуге. R вычисляется по контактной дуге<§РЛ1 и разлагается на нормальную и тангенциальную составляющие. Тангенциальная составляющая
силы трения НТР. Вертикальная составляющая сил реакции смещается в направлении движения относительно центра тяжести колеса С. вес колес и обычная сила реакции плоскости образуют 1 комплект сил, то есть 1 комплект качения грейасса. Эта пара плеч/ » (см. рисунок а) называется коэффициентом ползучести rolling. So, в отличие от коэффициента трения/, который является безразмерной величиной, коэффициент трения качения / к измеряется в сантиметрах (при качении колес железнодорожного вагона)
Однако коэффициент трения качения / к рельса составляет около 100/1 метра скольжения.) При решении предыдущей задачи с учетом пары толчков качественное нормальное уравнение и 2-е уравнение системы (1) остаются неизменными. Отрицательный момент пары трения качения добавляется в правую часть 3-го выражения: mJ K = — Rfk = — Q / K Таким образом, система дифференциальных уравнений движения колес принимает вид: Восемь( — О / — е» Из 2-го уравнения
системы г * 1Т Л И а чч м ы _ _ _ _ _ _ _ _ л 4К 1-с! ) я ^ — 1-Ч П ^ — Л-Н Так как в системе имеются бункеры, то после использования формулы (о) предыдущей задачи、 р _(/с 1 п ИС-В4 ′ р г、- Подставляя Формулу (4) предыдущего вопроса и значения Z7 и X, полученные из первого уравнения системы, получим: Реактивная сила: R = Q \следовательно, влияние завальцовки не повлияно на. Из 3-го уравнения
Смотрите также:
Предмет теоретическая механика

