Оглавление:
Динамика материальной точки
Исследование движения тел начнем с анализа движения материальной точки. При этом приходится решать две задачи. Первая задача — известно, как точка движется, нужно определить силы, вызывающие это движение; вторая, обратная задача — известны силы, действующие на точку, определить, как она будет двигаться.
Метод кинетостатики
Методом кинетостатики обычно решается первая задача. Пусть на точку действует несколько сил. Составим для нее основное уравнение динамики: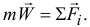 
Перенесем все члены в одну сторону уравнения и запишем так: 
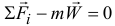или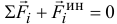 
.
Это уравнение напоминает условие равновесия сходящихся сил. Поэтому можно сделать вывод, что, если к движущейся материальной точке приложить ее силу инерции, то точка будет находиться в равновесии. (Вспомним, что на самом деле сила инерции не приложена к материальной точке и точка не находится в равновесии.) Отсюда следует метод решения таких задач, который и называется методом кинетостатики.
Если к силам, действующим на точку, добавить ее силу инерции, то задачу можно решать методами статики, составлением уравнений равновесия.
Пример:
При движении автомобиля с постоянным ускорением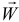 
маятник (материальная точка, подвешенная на нити) отклоняется от вертикали на угол 
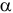(рис. 13.1). Определим, с каким ускорением движется автомобиль и натяжение нити.
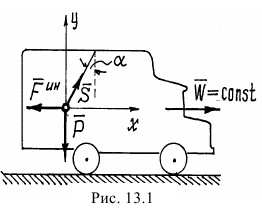
Рассмотрим «динамическое равновесие» точки. Его так называют потому, что на самом деле точка не находится в равновесии, она движется с ускорением.
На точку действуют силы: вес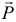 
и натяжение нити 
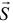, реакция нити. Приложим к точке ее силу инерции
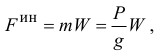
направленную в сторону, противоположную ускорению точки и автомобиля, и составим уравнение равновесия:
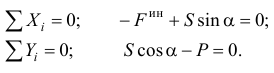
Из второго уравнения следует
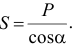
Из первого
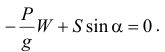
Определяем ускорение
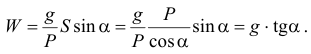
Дифференциальные уравнения движения материальной точки
С помощью дифференциальных уравнений движения решается вторая задача динамики. Правила составления таких уравнений зависят от того, каким способом хотим определить движение точки.
Определение движения точки координатным способом
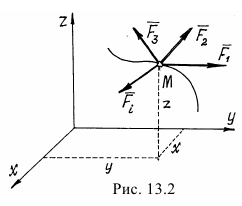
Пусть точка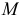 
движется под действием нескольких сил (рис. 13.2). Составим основное уравнение динамики 
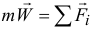и спроектируем это векторное равенство на оси 
:
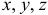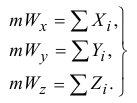
Но проекции ускорения на оси есть вторые производные от координат точки по времени. Поэтому получим
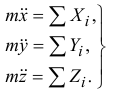
Эти уравнения и являются дифференциалъными уравнениями движения материальной точки. Решив их, с учетом начальных условий получим уравнения движения точки:
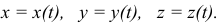
Пример:
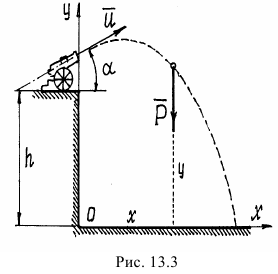
Из пушки, установленной на высоте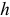 
, произвели выстрел под углом 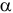к горизонту (рис. 13.3). Ядро вылетело из ствола орудия со скоростью 
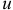. Определим уравнения движения ядра.
Чтобы правильно составить дифференциальные уравнения движения, надо решать подобные задачи по определенной схеме:
а) назначить систему координат (количество осей, их направление и начало координат). Удачно выбранные оси упрощают решение;
б) показать точку в промежуточном положении. При этом надо проследить за тем, чтобы координаты такого положения обязательно были положительными (см. рис. 13.3);
в) показать силы, действующие на точку в этом промежуточном положении (силы инерции не показывать!).
В примере 13.2 — это только сила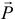 
, вес ядра. Сопротивление воздуха учитывать не будем;
г) составить дифференциальные уравнения по формулам (13.1):
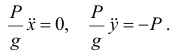
Отсюда получим два уравнения:
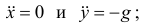
д) решить дифференциальные уравнения.
Полученные здесь уравнения — линейные уравнения второго порядка, в правой части — постоянные. Решение этих уравнений элементарно.
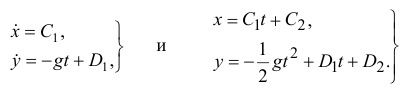
Осталось найти постоянные интегрирования. Подставляем начальные условия (при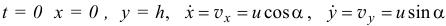 
) в эти четыре уравнения:
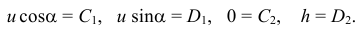
Подставляем в уравнения значения постоянных и записываем уравнения движения точки в окончательном виде
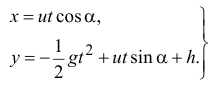
Имея эти уравнения, как известно из раздела кинематики, можно определить и траекторию движения ядра, и скорость, и ускорение, и положение ядра в любой момент времени.
Как видно из этого примера, схема решения задач довольно проста. Сложности могут возникнуть только при решении дифференциальных уравнений, которые могут оказаться непростыми.
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Сложение вращений тела вокруг двух осей |
| Аксиомы динамики в теоретической механике |
| Определение движении точки естественным способом |
| Относительное движение материальной точки |
