Оглавление:












Динамическое программирование (планирование)
- Динамическое программирование (планирование) Использование динамического программирования (планирование) Выберите лучший план для выполнения многошагового действия. для Многоступенчатые действия характеризуются течением времени. В дополнение к действию, которое, естественно, многоступенчатое (Например, долгосрочное планирование), со многими задачами.
- Искусственно разделен на этапы Возможно применение динамического программирования. Как правило, динамические задачи Программирование сводится к следующему: Есть контролируемая операция Разделить на (намеренное поведение) (естественное или искусственное) м шагов. Распределение на каждом этапе Перераспределение людей, участвующих в операциях по улучшению Общий результат.
Эти распределения динамические Программирование называется операционным управлением и определяется Письмо U. Людмила Фирмаль
Общая эффективность операции Показателем эффективности контроля является W (U). Кроме того, эффективность управления W (U) зависит от всего Набор элементов управления на каждом этапе операции: W = W (U) = W (U1, U2, …, UJ. (3,63) Контроль достигнут по индексу W Максимальное значение называется оптимальным управлением. оптимум Органы управления обозначены буквой U.
Оптимальное многоступенчатое управление процессом Он состоит из набора оптимальных пошаговых контролей. U = (U ,, U2, …, Um). (3,64) Цель динамического программирования — решить Оптимальное управление на каждом шаге C (i = 1, 2, …, m), таким образом Оптимальное управление всей операцией. Наиболее практичная задача Общий показатель эффективности W.
Общая эффективность действий на всех этапах операции (этапов): м w = Z (0i ‘(3,65) я = я Где (а — эффективность работы на i-м шаге. Для оптимального управления м w = maxZ ° V (3,66) Существа, которые решают задачи динамического программирования Это так. -Оптимизация выполняется последовательно Приблизительные два круга (итерация) от последнего шага Первая до последней операции — первая до последней -С следующего шага на первом круге.
Предыдущая, так называемая условная оптимизация Управление, потому что выбран условный оптимальный контроль, Максимальная эффективность была достигнута на всех предыдущих этапах Следующий шаг, другими словами, каждый шаг Контроль, обеспечивающий оптимальную непрерывность Операция, этот принцип выбора управления называется принципом оптимальность;
Это продолжается до первого шага, но с первого шага Шаг не имеет ничего раньше. После этого приобретенное состояние Оптимальное управление теряет условные знаки и Оптимальное управление, которое мы ищем. -Второй раунд оптимизации начинается с первого шага. Его оптимальное управление известно.
Выполнить условную оптимизацию на всех последующих шагах Управление, зная, что нужно сделать в каждом после оптимального управления многоступенчатым процессом Он состоит из набора оптимальных пошаговых контролей. U = (U ,, U2, …, Um). (3,64) Цель динамического программирования — решить Оптимальное управление на каждом шаге C (i = 1, 2, …, m), таким образом Оптимальное управление всей операцией.
Наиболее практичная задача Общий показатель эффективности W Общая эффективность действий на всех этапах операции (этапов): м w = Z (0i ‘(3,65) я = я Где (а — эффективность работы на i-м шаге. Для оптимального управления м w = maxZ ° V (3,66) Существа, которые решают задачи динамического программирования Это так. -Оптимизация выполняется последовательно.
Приблизительные два круга (итерация) от последнего шага Первая до последней операции — первая до последней -С следующего шага на первом круге Предыдущая, так называемая условная оптимизация Управление, потому что выбран условный оптимальный контроль, Максимальная эффективность была достигнута на всех предыдущих этапах Следующий шаг, другими словами, каждый шаг Контроль, обеспечивающий оптимальную непрерывность.
Операция, этот принцип выбора управления называется принципом оптимальность; -Это продолжается до первого шага, но с первого шага Шаг не имеет ничего раньше. После этого приобретенное состояние Оптимальное управление теряет условные знаки и Оптимальное управление, которое мы ищем. -Второй раунд оптимизации начинается с первого шага.
Его оптимальное управление известно. Выполнить условную оптимизацию на всех последующих шагах Управление, мы знаем, что нам нужно делать на всех послепродажных Масса и стоимость груза типа i-ro (условная единица) индикатор условно Блок пирог Тип груза, я 1 10 20 2 16 50 3 22 85 4 24 96 Решения В этом примере нет естественного разделения операций Следуйте инструкциям для загрузки.
Такое разделение необходимо для решения проблемы. Рекомендуется вводить его искусственно. Различные типы авиационных объектов. Есть четыре таких шага. Порядок расчета следующий: В первом раунде оптимизация начинается с четвертого типа Груз-4-й шаг. самолет Загрузка только с четвертым типом предмета. В этих условиях Максимальное значение нагрузки для четвертого шага w4 = f; (0) = max {x4, C4} (3.71)
В условиях, вытекающих из условий (3.69) и (3.70), * 4P4 * G; dg4 = 0,1,2, … Из первого условия Из второго условия xA может быть только целым числом. Следовательно, целая часть полученной дроби получается как x4. f | — | W6 | = 3. привет там Это последнее условное оптимальное управление. Четвертый шаг: и 4 = * 4 = ч. Максимальное значение нагрузки при такой нагрузке.
Определяется по формуле (3.71). ω. : F (G) = максимум {3 · 96} = 288. Перейти к предыдущему третьему шагу. Самолет загружен четвертым типом предмета, Третий тип предмета. Когда вы получите третий тип объекта х3 на этом этапе, Количество объектов четвертого типа Вес не может быть превышен (G- * 3P3).
Максимум этого Нагрузка составляет ФА (G- * 3P3). Максимальная стоимость груза 4-й и 3-й типы, определяемые по формуле Используйте пределы (3.69) и (3.70) из следующего уравнения (3.68): / 3 (G) = Макс {* 3C3 + / 4 (G- * 3 P3)} (3,72) в 0 <x3 < G (3,73) Расчет по формуле (3.72) выглядит следующим образом. Предел (3.73) 83 0 <x3 < 22 Это означает, что x} не может принимать больше значения. х} = 0,1,2,3.
Рассчитано для каждого из этих четырех значений Значение в фигурных скобках в формуле (3.72) и в футах (G) Рассчитаем по формуле (3.71): x} \ {V85 + /; (83-v22)} {θ · 85 + / 4 (83-0 · 22)} = {θ + / 4 (83)} = — | θ + = {θ + 288} = 288; 83 {ΐ ・ 85 + / 4 (83-1 · 22)} = {85 + / 4 (61)} = | 85 + = {85+ 192} = 277; 24 61 96 U 24 96 = {2 85 + / 4 (83-2 22)} = {70 + / 4 (39)} =] 70 + = {170 + 96} = 266; 39 24 96 {3-85 + / 4 (83-3-22)} = {255 + / 4 (17)} = J255- = {255 + 0} = 255. 17 24 96
- Далее рассчитывается максимальное полученное значение. f3 (G) = максимум (288; 277; 266; 255) = 288. Соответствует этому наивысшему значению Загрузка x3 = 0 приведет к условно оптимальному управлению Третий шаг: с = * 3 = 0. Затем перейдите ко второму шагу и загрузите Второй тип объекта — и для него мы находим аналогичным образом f2 (G) = 288 и соответствующий U2 = x2 = 0
Точно так же первый шаг / j (G) = 308hUi = xi = 1. Первый шаг — условное оптимальное управление В то же время оптимальным является управление C : Вы; = и, = я. Второй раунд оптимизации начинается с первого шага Последний. Потому что мы знаем его оптимальное управление На первом этапе требуется одна единица груза первого типа.
Кроме того, будет распространяться только то, что осталось в остальных типах. Людмила Фирмаль
Груз, т.е. G ‘= 83-1 · 10 = 73 ед. Выполните тот же расчет, что и выполненный На первом круге мы постоянно получаем лучшее Второй, третий и четвертый этап управления: и / = o; u3 ‘= o; и / = 3. Оптимальное управление обеспечивает: Максимальная общая стоимость груза рассчитывается по Формула (3,68): W = 1 ・ 20 + 0 ・ 50 + 0 ・ 85 + 3 ・ 96 = 308
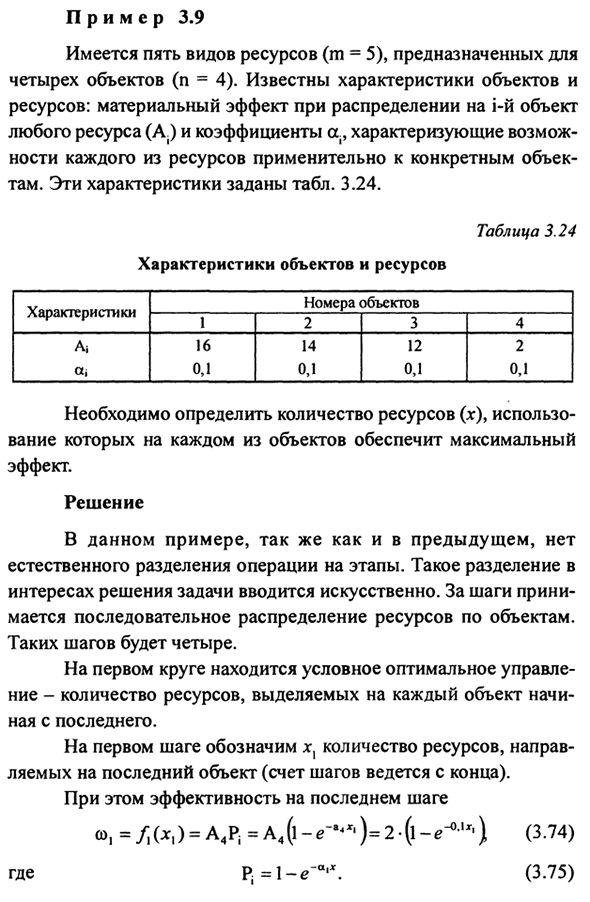
В рассматриваемом примере оптимизация Реализуется из любого типа предмета. Ваш заказ В соответствии с общей идеей динамического программирования. Пример 3.9 Существует пять типов ресурсов (t = 5). 4 объекта (n = 4). С характеристиками объекта Ресурс: значительный эффект при распространении на i-й объект Произвольный ресурс (А.) и коэффициент А, характеристики Функция каждого ресурса по отношению к конкретному ресурсу Объект.
Эти характеристики приведены в таблице. 3,24. Таблица 3.24 Характеристики объекта и ресурса 1 функция Любовь Любовь Номер объекта 1 16 0,1 2 14 0,1 3 12 0,1 4 2 0,1 Вам необходимо определить количество ресурсов (х). Максимальное значение, гарантированное использованием на каждом объекте Эффект. Решения В этом примере, как и в предыдущем примере, нет Разделите операции на этапы естественно.
Сплит как Прибыль для решения проблемы вводится искусственно. О процедуре Последовательное распределение ресурсов по объектам допускается. Есть четыре таких шага. Условно оптимально на первом круге Управление-количество ресурсов, выделенных для каждого объекта Начните с конца. На первом этапе, dg, количество ресурсов, Отправляется на последний объект (шаги отсчитываются с конца).
В то же время эффективность на последнем этапе ω, = /, (,) = A4P (= A4 (1st- ^) = 2 (1- ^ ‘* *) (3.74) Где P ^ l-e «». (3,75) Поскольку это количество, значение xx неизвестно. Ресурсы, оставленные от условного оптимального управления 2-й шаг от конца (2-й от конца). Изучите все возможные значения χχ для каждого Вычислить / | (χ,) по формуле (3.74). Как видно из рассматриваемого условия, χχ может принимать значение О, 1, 2, 3, 4, 5.
Выполните расчеты по этим значениям (таблица 3.25). Таблица 3.25 Возможное значение x и эффективность fx (xx) 1 х 0 1 2 3 4 5 / л (* л) я 0 0,190 0,363 0,518 0,6590,787 1 На втором этапе (с конца) выделяются ресурсы x2 Предпоследний объект и соответствующая эффективность на этом этапе В дополнение к эффекту второго шага, ω2 должен быть принят во внимание.
Эффект условного оптимального управления Первый (с последнего) шага: ω2 = ΑΒ.Ι [ΐ-β — (* — »)]. (3,76) Максимальный эффект, полученный в два этапа Аналогично уравнению (3.74): / 2 (jc2) = max ^ 3 (l- ^ MX2 «x,)) + A4 (l- ^ a4JC ‘)}’ <3’77) 0 <x1 <x2. Потому что х2 — это количество целевых ресурсов Поражение предпоследнего объекта, тогда x2> χχ. Исходя из этого, делайте предположения обо всем возможном Рассчитано для значений х2 (х2 = 0, 1, 2, 3, 4, 5) и каждого из них Эффективность (Таблица 3.26).
В то же время, значение χχ (условное Оптимальное управление), f2 (x2) достигает максимума. с того времени Это зависит от x2, обозначенного x} (x2) и показанного в таблице. 3,26. Возможное значение х2, максимальная эффективность И их соответствующие значения χλ (χ2) Я * 2 0 1 2 3 4 5 / ife) 0 +1150 2175 3108 3954 4722 х \ (хг) 1 0 0 0 0 0 О 1
Кроме того, аналогичным образом для всех возможных значений * 3 f3 (x3) и x2 (x3) являются расчетными вкладками. 3,27. Таблица 3.27 Возможное значение jc3, максимальная эффективность f3 (x3) И соответствующее значение х2 (х ^ _ 0 1 2 3 4 5 AM 0 1330 2541 3508 4680 5804 * 2 (* 3) 0 0 0 2 2 2 1 Аналогично условно оптимально Управление четвертым (с конца) шагом.
Но на этом этапе Достигните начального (начального) значения количества единиц Ресурсы (единицы) для всех объектов (t = 5), затем Величина xg определяется только для x4 = 5. Как показывает расчет, χ3 (* 4 = 5) = 2. Второй раунд оптимизации начинается в обратном порядке (От четвертого шага к первому шагу). Первый для всех Объект имеет 5 единиц и после назначения ресурса одному из ресурсов Объект подлежит условно-оптимальному управлению.
Для всех остальных оставьте * 3 (x4) = 2 единицы. Контроль четвертого (с конца) шага А / = * 4 = 5-2 = Зед.р. Оптимальное управление третьим (с конца) шагом При распределении оставшихся 5-2 = 3 ед. Принцип оптимальности был сохранен. Как вы уже знаете, Как показывает анализ в таблицах 3.25, 3.26 и 3.27, Если xr = 2 x2 (x3) = 0, Когда х2 = 0 хх (х2) = 0. Следовательно, x * = x, * = 0.
Следовательно, оптимальное целевое распределение U / = 3 единицы, U / = 2 единицы, U / = 0 единиц, U, * = 0 единиц Общий урон W = 16 ・ (1-e *>] 3) + 14 ・ (1-e * 1 2) + 12 ・ 0 + 2 ・ 0 = 6,68 Пример 3.10 Единицами ресурса являются 7 (t = x0 = 7) Распределяется между двумя компаниями-партнерами в несколько этапов Операция. Первая компания назначена у, а вторая компания (х-у) Единица ресурса. Операция выполняется в три этапа (n = 3).
На каждом этапе ресурсоэффективности Первая компания g (y) = 0.4y2, вторая компания h (x-y), Где g и h — соответствующие факторы производительности От компании. Для потребления ресурсов на каждом этапе В процессе работы количество ресурсов для первой компании составляет 0,6y, до второго -0,9 (x -y). Ресурсы будут перераспределены к началу следующего этапа.
Нужно найти оптимальное распределение ресурсов Каждый шаг операции и общая эффективность. Решения Эта задача имеет естественное разделение. Шаг операции-этап действия. Есть три таких шага. На каждом этапе компания эффективна, Пропорционально выделенным ресурсам: первая компания Эффективность g (x0), секунда h (x0-y0). После первого этапа действий (шаги по решению проблемы) Общая эффективность обеих компаний «. = / J (* У0) = g (> 0) + b (* 0-Vn) (3.78)
Во время работы доступные ресурсы расходуются, В результате в конце каждого этапа действий появляется ряд Ресурсы первой компании сокращены до ay0 (0 <a <1) Во-вторых, максимум b (x0-y0), 0 <b <1. Где а и б Фактор, указывающий на экономию ресурсов Конец каждого этапа. Остальные ресурсы к началу каждого следующего шага Обе компании c ^ gO ^ + hix.-y,), (3.80)
Общая эффективность в два этапа эксплуатации: Ф »У» У,) = 8 (Йо) + ч (* о к Йо) + г (В,) + ч (. «Ud- (3 ・ 8О Аналогичным образом общая эффективность η этапа эксплуатации Ф »уо >> Ί> -> yn-v) = ^ o) + h (от xo до yo) + — + + g (yn.1) + h (xn.1-yn_1). (3,82) Вам необходимо распределить ресурсы по всему предприятию Общий эффект на каждом этапе Операция была максимальной. Условно оптимально в первом туре расчета Управление.
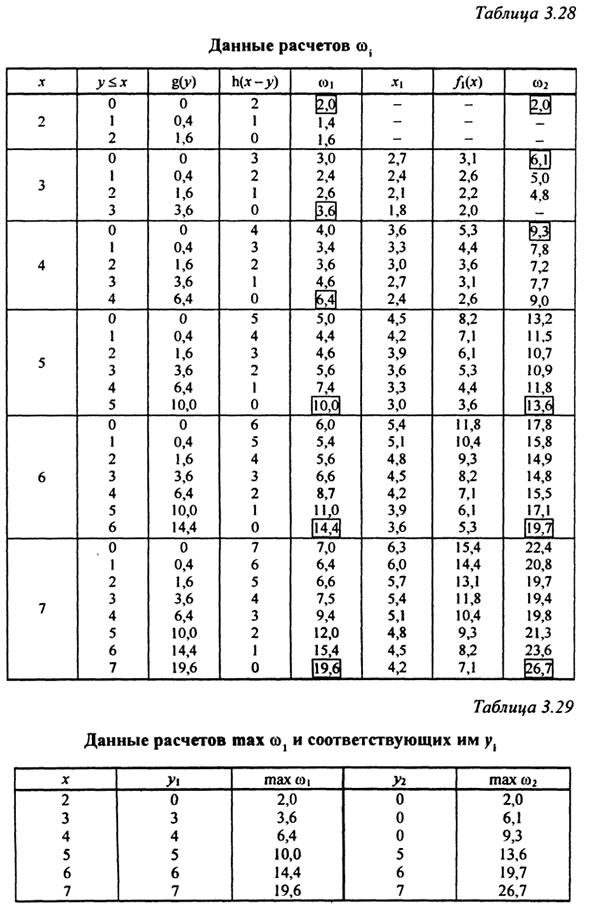
Первый шаг (с конца) по формуле (3.74) Эффективность ω определяется для всех возможных значений от 0 до χ. Если y ,) Tab. 3,28 (6-й ряд). Далее по полученным значениям x и s Рассчитано интерполяцией по 3.29, х по таблице Соответствующее значение f | (x) заносится в таблицу. 3,28 (7-я колонка). Далее общая эффективность двух действий Первый шаг: ω2 = ω, + / (*). (3,83) Результаты расчета ω2 приведены в таблице. 3,28 (8 дней Column).
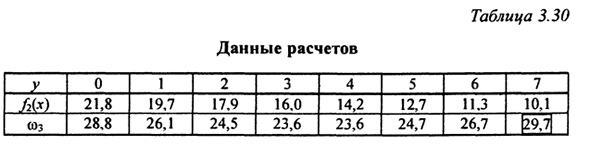
Максимальное значение ω2 в таблице. 3.28 раунд Экспортируется с прямоугольником и соответствующим значением Таблица y2. 3,29 (4-й и 5-й столбец). Точно так же (с конца) на третьем этапе x2, f2 (x), ω3 = ω, + f2 (x). Потому что этот шаг имеет только одно значение Если χ = x0 = 7, расчет выполняется только при χ = 7 (таблица 3.30).
Из анализа таблицы. 3.30 условно оптимально Контроль третьего шага, соответствующего максимуму Эффективность (заключенная в прямоугольник) равна 7. На этом этапе вы знаете оптимальный контроль одновременно: U * = y = 7. Начинается второй раунд оптимизации (в обратном порядке).
Первоначально х0 = 7, оптимальный Управление с начала (с начала) y * = 7, затем следуйте таблице. 3,28 хх = 4,2. Это значение χλ в таблице. 3.29 Найти лучший Управление со вторым шагом y * = 0. Аналогично определите y3 = 3,8. Поэтому на первом этапе эксплуатации первая компания На втором этапе всем 7 единицам должны быть выделены ресурсы — 0 единиц и 3-й — 3,8 ед.
Это максимум Общая эффективность операции равна по всему выражению (3,82) W = 0,4 В + (7-7) + 0,4 O2 + (4,2-0) + 0,4 (3,8) 2 + (3,8-3,8) = = 19,6 + 4,2 + 5,8 = 29,6.Перераспределяется между компаниями. Количество ресурсов, оставшихся в начале второго этапа Операция равна (*,): Xl = ay0 + b (xQ-y0 \ (3.79) Или иначе: x \ = Y \ * (χ \ ~> Ί >> Где 0 <y1 <xr Всего по окончании второго этапа эксплуатации эффект
Смотрите также:
| Методы оптимизации: линейное программирование | Теория вероятностей и математическая статистика. Основные понятия |
| Нелинейное программирование (планирование) | Основные теоремы теории вероятностей |

