Оглавление:




Динамическое (многопериодное) бюджетное ограничение
- Динамические (многопериодные) бюджетные ограничения Если домохозяйство открыто в течение двух периодов, продолжите обсуждение, используя формальную модель. Эти периоды не обязательно должны быть одинаковыми. Вы можете думать о первом периоде как о «настоящем», а второй период как о «будущем».
- Также удобно думать о нулевом периоде как о «прошлом». Эта упрощенная формулировка, известная как двухпериодная модель, отражает все важные аспекты принятия решений с учетом временных факторов и в то же время очень удобна. (Продолжая эмпирические исследования, он становится более реалистичной многопериодной моделью.) Бюджетное ограничение для двухпериодной модели.
Пока эта проблема изучается на абстрактном уровне, не имеет значения, сколько лет длится каждый период. Людмила Фирмаль
Во-первых, предположим, что в прошлом не было ценных бумаг в домашнем хозяйстве (B0 = 0), и что в конце жизни в домашнем хозяйстве не было ценных бумаг (B2 = 0). На этом этапе мы исключаем наличие мотивации оставлять наследство потомству и предполагаем, что индивид не может умереть как должник (то есть B2 не может быть меньше нуля).
При этих допущениях -BQ = B] = Sv, поэтому сбережения в первом периоде равны стоимости облигации на конец первого периода. Аналогично, поскольку B2-Bx = S2 и B2 = 0, мы знаем -Bx = S2. Значит экономия в первом периоде 5 = Z? Вы можете видеть, что оно равно «предотвратить сохранение» во втором периоде S2 — Wu.
Это приводит к важному выводу о том, что если домохозяйство родилось и умерло без ценных бумаг, сбережения в первом периоде равны сбережениям «минус» во втором периоде (S2–5). Таким образом, решение, которое принимают домашние хозяйства, заключается не в том, когда они экономят или арендуют, а когда.
Если домохозяйство сберегает в молодом возрасте (период 1), сбережения должны быть потрачены в старости (период 2), а если оно арендовано в молодом возрасте, оно должно быть сохранено в старости. Согласно определению сбережений: 5 = Vx-C, -O, -C, = Bx; (4.4) S2 = V2-C, — * Q2 + rBx-C2. (4.5) Поскольку S2 =, используйте соотношения (4.4) и (4.5), чтобы получить C, -Q {= Q2 + / • ((?, -С,) -Cj или просто после преобразования.
W представляет богатство. Коэффициент (4.6) является многопериодным бюджетным ограничением для домашних хозяйств. Это означает, что текущая стоимость потребления должна быть равна текущей стоимости продукции.
Приведенную стоимость продукции можно также рассматривать как богатство домашнего хозяйства (W ^ j) в начале первого периода (до того, как домашнее хозяйство определит потребление в первом периоде). Основные условия, описываемые этими отношениями, могут быть обоснованы на интуитивном уровне. Домохозяйства в определенный период могут потреблять больше дохода.
- Но в течение всей жизни потребление, очевидно, не может превышать размер средств, которые они имеют, и, как мы договорились, домохозяйства потребляют не меньше, чем они, и наследство. Не выходит Условие текущей стоимости означает, что семья может выбрать распределение потребления, которое соответствует требованиям для каждого периода (C и C2).
Домохозяйства должны жить в течение этого периода, а не в течение этого периода. Эта модель может включать два новых предположения. Например, если домохозяйство, которое уже получило ценные бумаги в качестве наследства, начало существовать, это означает, что домохозяйство может провести остаток своей жизни.
Текущая стоимость потребления равна текущей стоимости дохода. Людмила Фирмаль
Во-вторых, бюджетные ограничения принимают форму: 4 Это бюджетное ограничение можно описать более сходным образом с бюджетным ограничением стандартной теории потребления. Пусть P2 будет единицей потребления за первый период и иеной за потребление второго периода.
Обратите внимание, что для увеличения потребления на втором Периоле Элину вам необходимо уменьшить погребение первого периода на 1 / (1 + г) единиц (т.е. увеличить эту сумму экономии). Вот так. P} ■ = 1 (1 + / ■). Очевидно, что цена потребительских товаров первого периодита сводит потребление первого периода к одному.
Это позволяет создать ценовую структуру (которую можно назвать динамическим многопериодным ценообразованием). Вы можете использовать эти цены, чтобы записать бюджетные ограничения ka * РхС, + />, С, PyQ {+ P} Q}. Это выглядит как нормальное бюджетное ограничение для потребителей. (Wr) (Ура) Где (1 + r) B * — основной B0 и процент rf?
Значение по наследству B0 за первый период, в том числе 0. Если домохозяйство открыто в течение многих периодов, бюджетные ограничения принимают следующую форму: (4L) V ^ J (ур) C | + т-1 — (Ur) * 0 + OI + Ql (Ура) (, ♦,) X__IV, .7 «-I 1 * (4.8) Это соотношение можно получить, непрерывно используя соотношение (4.2) в периоде r (r-1,2, …, 7).
5 Если домохозяйство хочет передать наследство следующему поколению, оно не будет тратить все богатство жизни. Пусть BQT будет значением наследования к концу периода T. После этого богатство остается таким же, как в формуле (4.8), а дисконтированная стоимость потребления равна -BQT / (\ + r) T.
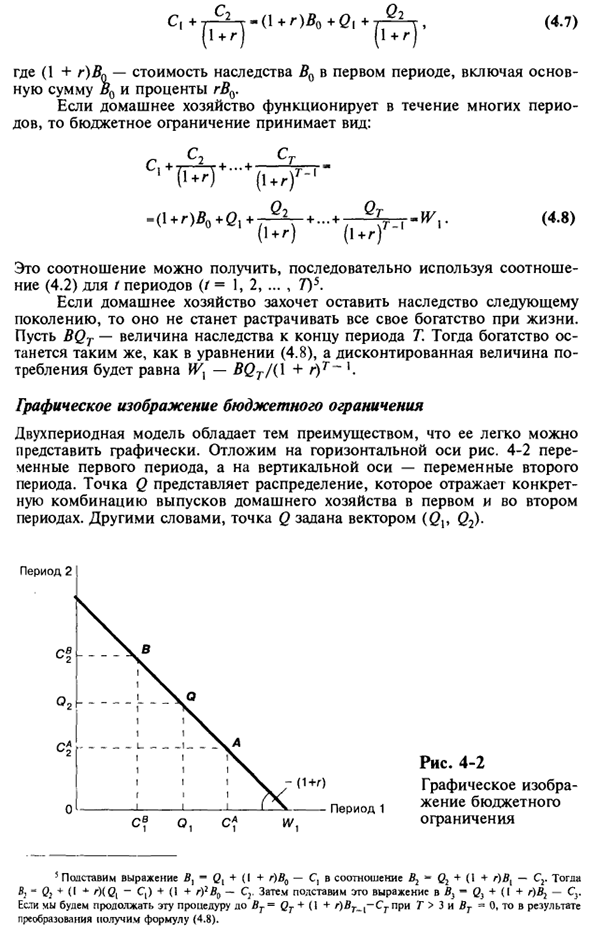
Диаграмма бюджетных ограничений Преимущество двухпериодной модели состоит в том, что ее легко представить графически. Поместите на горизонтальную ось Рисунок 4-2 первую переменную периода и вертикальную ось-переменную второго периода. Точка Q представляет собой распределение, которое отражает конкретную комбинацию выбросов домашних хозяйств в первом и втором периодах.
То есть точка Q задается вектором (() ,, Q2). Рис. 4-2 Диаграмма бюджетных ограничений г (1 + о Период 2 Период 1 5 Подставим формулу D, -Q {+ (I + r) B0-C в соотношение B2-Q2 + (I + r) Bl-C. Тогда B, -Q} * (I * ‘) ( 3 и BT_-St при г = «0 Далее, результат преобразования дает уравнение (4.8). Бюджетное ограничение в соотношении (4.6) можно легко нарисовать на графике, если оно записано в виде C2 = (? 2 ~~ (1 + r) Cx + (1 + r) Qv.
Линия под углом, наклон- (1 + g) проходит через точку ((?, Q2). Эта линия — все возможное потребление (С ,, С ^), которое удовлетворяет многопериодному бюджетному ограничению. Домохозяйства могут выбрать любой вектор потребления в этой строке, изменив будущий доход на сегодняшний день, снизив ссуду до g процентов или менее, или ссудив средства на r процентов сегодня.
Для получения будущих доходов r измеряет возможность изменения текущего потребления в будущем или наоборот путем приобретения ценных бумаг. Если домохозяйство выбирает потребление в точке A на рисунке 4-2, оно будет вынуждено занять в первом периоде, потому что С ^> Qv, что домохозяйство станет чистым должником к концу первого периода Ясно.
Результат должен быть меньше, чем во втором квартале, потому что вы должны заплатить долг (как вы можете видеть на рисунке). Следовательно, нисходящая прямая линия отражает основную проблему динамического отбора. Для определенных производственных путей семьи могут увеличить текущее потребление только за счет будущего потребления.
Напротив, в точке B семья ограничивает потребление в первом периоде (Cf <(?)) По сравнению с более высокими уровнями потребления в будущем. Скидка на потребление находится на пересечении бюджетной линии и горизонтальной оси (точка Wj). Обратите внимание, что Wy = Q \ + (? O / P + характеризует благосостояние домохозяйства.
Смотрите также:
| Национальное потребление и сбережения | Принятие решений домашними хозяйствами |
| Домашнее хозяйство — основная ячейка экономики | Теория потребления с постоянным доходом |
Если вам потребуется помощь по макроэкономике вы всегда можете написать мне в whatsapp.

