Оглавление:





Дифракция Френеля
- Дифракция Френеля. Если точка P ищет источник света и интенсивность света находится на конечном расстоянии от экрана, только небольшая часть волнового фронта будет играть интегрирование (59.2), чтобы определить интенсивность в точке P , Прямая линия, соединяющая источник света с точкой P.
Дифракционное явление, в котором роль играет только небольшая часть волнового фронта, называется дифракцией Френеля. Рассмотрим дифракцию Френеля на экране. С этим свойством роль играет только небольшая часть края экрана (в определенной точке P). Однако в точке Q и точке наблюдения P мы ищем значения интенсивности света.
Указывает расстояние от источника света Людмила Фирмаль
Наконец, выберите начало координат O на линии края экрана. Положения всех трех осей затем четко определены. Q до начала Представляется символом Dq, координата z точки P наблюдения является символом Dp, а координата z, то есть расстояние до плоскости xy, является символом d.
Согласно геометрической оптике, свет может достигать только точек на плоскости xy, области под плоскостью xy — это области с тенями (геометрические области теней) в соответствии с геометрической оптикой. Далее определяют распределение интенсивности света Для экранов вблизи границы геометрических теней, т.е. для малых значений d (по сравнению с Dp и Dq).
- Отрицательный d означает, что точка P находится в области геометрической тени. Как интеграционный аспект (59.2) Полуплоскость, проходящая через край экрана перпендикулярно плоскости xy. Координаты x и y точек на этой поверхности связаны друг с другом соотношением x = y tan a (где a — угол между линией на краю экрана и осью y), а координата z положительна.
Волновое поле, генерируемое на расстоянии Rq от источника Q, пропорционально коэффициенту exp (ikRq). Следовательно, поле и поверхность интегрирования пропорциональны В достаточно маленькой области край экрана всегда можно считать простым. Ниже это означает, что ниже края экрана Прямой участок.
перпендикулярная к нему Выберите Людмила Фирмаль
Рисунок 11 Выберите плоскость, чтобы пройти в качестве плоскости ху Разрежьте источник света Q (рисунок 11) по краю экрана. Плоскость Xz, , чтобы пройти И ~ опыт В интеграле от R (59,2) R = ijy2 + (z-d) 2+ (Dp-ytga) 2.
Для подынтегральных величин медленно меняющиеся факторы не являются значительными по сравнению с экспоненциальными факторами Следовательно, 1 / R можно считать постоянной, вместо дфн пишет дидз. Далее, точка P поле + оо оо Up rsj n exp Сью О ik J (Dq + ytga) 2 + y2 + z2 + + yj (Dp-ytg a) 2 + у2 + (z-d) 2] dydz. (60,1) Как уже упоминалось, точка P в основном о Из точки на плоскости интегрирования непосредственно рядом с О.
Следовательно, интеграл (60.1) мал (по сравнению с Dq и Dp) значения y и z Могу написать L ————————— 2. 2 Dq + ytga) 2 + y2 + z2 «Dq + v z + ytga, Zj-джа Dp-ytga) 2 + y2 + (z-d) 2 & Dp + V ——— ytga. Заменить это на (60.1). Потому что нас интересует только поле Постоянная постоянная как функция расстояния d exp [ik (Dp + Dq) \ exclude; интеграл по dy также дает выражение. Не включайте d, опустите его.
Тогда найдите: OO G- П и ж ж + ж р (* — *?) Это выражение также может быть записано в следующей форме: дюжина ик 2 (Дп + Дк о / exp ik (1/2) [(1 / 1D / pD + P1 + / D1 / q) Dzq-d / Dp \ ‘dz. (60,2) Интенсивность света определяется квадратом поля, квадратом Модуль | PR | Так что найти силы Фактор интеграции не важен.
Умножьте формулу сопряженного, чтобы получить один. Очевидная замена для интеграла где W = D кД 2 дп (дк + дп) Следовательно, сила в точке Р равна 7 = о уу> 2др] Io 2 (C («2) + i) 2+ (s (w2) + i)! (60,4) (60,5) где C (z) = J cos rj2drj ^ S ‘(z) = J sin r] 2dr] Ах ах Это так называемый интеграл Френеля.
Уравнение (60.5) решено Определить задачу, интенсивность света как функцию Значение d / o является интенсивностью области, освещаемой точкой Достаточно далеко от края тени, т.е. w 1 (в определенных пределах) w os C (os) = S (os) = 1/2). Геометрическая область тени соответствует отрицательной ш.
Нетрудно определить асимптотику функции I (w) Отрицательное абсолютное значение w с большим абсолютным значением. Для этого выполните следующие действия: Интегрировать по частям, др] = 2i \ i + J_ f eir] 2dn 2 i J rj2 ‘ N N Снова закрепите в правой части равенства частей и продолжите этот процесс, чтобы получить ряд степеней 1 / | th |. OO [e ^ dr] = e ™ 2 (—- J — + — J-s J V 2i \ w \ 4 | gi | / \ w \ (60,6)
Эта форма бесконечного ряда не сходится, но при больших значениях \ w \ значение ее непрерывного члена быстро уменьшается, поэтому его первый член представляет левую функцию достаточно большую. \ w \ (этот ряд называется асимптотическим).
Поэтому для интенсивности I (w) (60,5) получается следующая асимптотическая формула, подходящая для больших отрицательных значений. значение w: ! = я б- <60-7> Геометрическая область тени, вы можете видеть, что это далеко от нее Сила края стремится к нулю обратно пропорционально квадрату расстояния от теневого края.
Теперь рассмотрим положительное значение w, то есть регион На плоскости ху. Написать + оо / «* *, = /» ***, — / L h = (1 + o f— —W —oo —oo W Для достаточно большого w можно использовать асимптотическое представление интеграла в правой части уравнения. о / l h th (1+,), /! (60,8) Подстановка этого уравнения в (60.5) дает: / = / о ^, 1 грех (w2-7g / 4) (60,9) Таким образом, в области освещения от края тени, Поскольку существует неограниченный ряд сильных сторон, отношение /// о будет изменяться в обоих направлениях устройства.
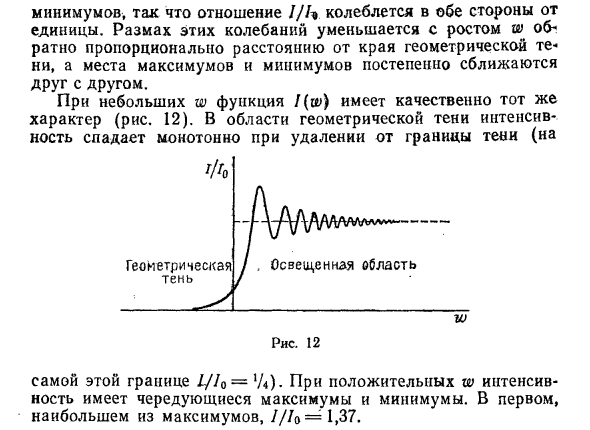
Амплитуда этих колебаний уменьшается с увеличением w обратно пропорционально расстоянию от края геометрической тени. Высокие и низкие места постепенно приближаются. Для малых w функция I (w) качественно одинакова. Лактор (рисунок 12).
В области геометрической тени интенсивность Монотонно уменьшается с расстоянием от теневой границы (эта граница /// o = 1/4). В случае положительного w интенсивность повторяется поочередно с высокой и низкой. Максимальное значение начального максимального значения /// o = 1.37.
Смотрите также:
| Пределы геометрической оптики | Дифракция Фраунгофера |
| Дифракция в физике | Запаздывающие потенциалы в физике |

