Оглавление:






Дифракция Фраунгофера
- Дифракция Фраунгофера. Особый интерес в физических приложениях представляет явление дифракции, возникающее при попадании лучей параллельной плоскости на экран. В результате дифракции луч теряет параллельность, и свет появляется и распространяется в другом направлении.
Ставит задачу определения распределения направлений интенсивности Дифрагированный свет на большом расстоянии за экраном (постановка этого вопроса соответствует так называемой дифракции Фраунгофера).
Задачи могут быть решены на основе Пройдите общую формулу Людмила Фирмаль
Кроме того, он снова ограничивает себя в случае небольших отклонений от геометрической оптики. Небольшой угол отклонения (угол дифракции) от исходного направления луча. (59.2), предел источника света и точку наблюдения бесконечно далеко от экрана. ха
Особенностью рассматриваемого случая является тот факт, что при интегрировании, которое определяет интенсивность дифрагированного света, существенным является весь волновой фронт, на котором выполняется интегрирование (в отличие от дифракции Френеля, волновой фронт у края экрана). Важна только часть) 1). Тем не менее, легче рассмотреть вопросы, которые были подняты.
- Используйте общую формулу (59.2). U указывает поле за существующим экраном При строгом соблюдении геометрической оптики. Это плоская волна и ее сечение 1) Стандарты дифракции Френеля и Фраунгофера можно легко получить, вернувшись к уравнению (60.2) и применив, например, ширину зазора (вместо края изолирующего экрана).
Интеграция через dz (60.2) В то же время диапазон составляет от 0 до a. Дифракция Френеля соответствует ситуации, когда для показателя степени подынтегрального выражения требуется член z2, а верхний предел интегрирования можно заменить на oo. Должно быть для этого ка (- +> 1. V Dp Dq J Наоборот, если обратный знак находится в этом неравенстве, член z2 Опущено, это соответствует случаю дифракции Фраунгофера.
Каждая такая плоскость является плоским волновым фронтом Людмила Фирмаль
Однако есть область (соответствующая непрозрачной «тени») Экран) имеет поле, равное нулю. Обозначим через S плоскую часть сечения, где поле u ненулевое. , поэтому u = const по всей области S. Но на практике волны с ограниченной плоскостью Диапазон поперечного сечения не может быть строго плоским (См. §58).
Пространственное разложение Фурье включает в себя Компоненты с волновыми векторами в разных направлениях, Это причина дифракции. Развернуть поле u двумерного интеграла Фурье по координатам В плоскости поперечного сечения волны есть y и z. Для компонентов Фурье -II щ iqrdydz, (61.1)
Где q — постоянный вектор в плоскости yz. Интегрирование фактически выполняется только в той части S плоскости yz. ты отличен от нуля. Если k — волновой вектор падающей волны, волновой вектор соответствует компоненте поля k ‘= k + q. Таким образом, вектор q = k ‘-k определяет изменение волнового вектора света при дифракции.
Поскольку абсолютное значение k = k ‘= co / s, малый угол дифракции wu, 6Z в плоскостях xy и xz связаны с компонентами вектора q связь Яу = Qz = -0z- (61,2) C C Небольшой отход от геометрической оптики Поскольку уравнение ni (61.1) решает проблему, можно предположить, что расширение поля ni соответствует истинной компоненте поля дифрагированного света.
Распределение интенсивности рассеянного света Делится на 2 | uq | 2 как функция от q. Количественная связь с интенсивностью падающего света JJ Uq dy dz = j j (61-3) (Ср. (49,8)). Это показывает, что относительная интенсивность дифракции к элементу телесного угла do = dQydQz определяется как Рассмотрим дифракцию Фраунгофера от двух экранов, которые «дополняют» друг друга.
Первый экран имеет отверстия, а второй экран имеет непрозрачные отверстия. U и u представляют дифрагированное световое поле На этих экранах (одинаковый падающий свет в обоих случаях). Поскольку они выражены как целое (61.1), Сфотографируйте площадь отверстия экрана, отверстия обоих экранов дополняют друг друга по всей плоскости, сумма U (!), (2) risq + Uq — компонент Фурье экрана, то есть поле, полученное в отсутствие простого падающего света.
Но падение Свет — это постоянная точная плоская волна U umoteo n, yaine narartsorpsar mein elvarpan (!), (2) nq + ich = U для Ненулевой q. Поэтому мы имеем Или для соответствующей силы, | Uq ^ | 2 = l ^ q ^ 2 для q ^ 0 (61,5) Это означает, что дополнительный экран дает такое же распределение интенсивности дифрагированного света (так называемый принцип Бабине).
Вот один интересный результат принципа. Бабин. Представьте себе черное тело, то есть тело, которое полностью поглощает весь поступающий свет. Согласно геометрической оптике, когда такой объект освещается, за ним образуется геометрическая теневая область, а его площадь поперечного сечения равна Равен с площадью поперечного сечения тела в направлении, перпендикулярном падающему направлению света.
Наличие дифракции Однако это приводит к частичному отклонению света от его первоначального направления. В результате на больших расстояниях позади тела нет тени, и есть некоторые тени вместе со светом, распространяющимся в первоначальном направлении. Количество света, которое распространяется под небольшим углом по отношению к исходному направлению.
Легко определить Говорят, что интенсивность этого рассеянного света. По этой причине, согласно принципу Бабина, Уменьшенный из-за дифракции в рассматриваемом теле, Равное количеству света, которое отклоняется во время дифракции от отверстия, врезанного в непрозрачный экран, его форма и площадь соответствуют форме и площади поперечного сечения тела.
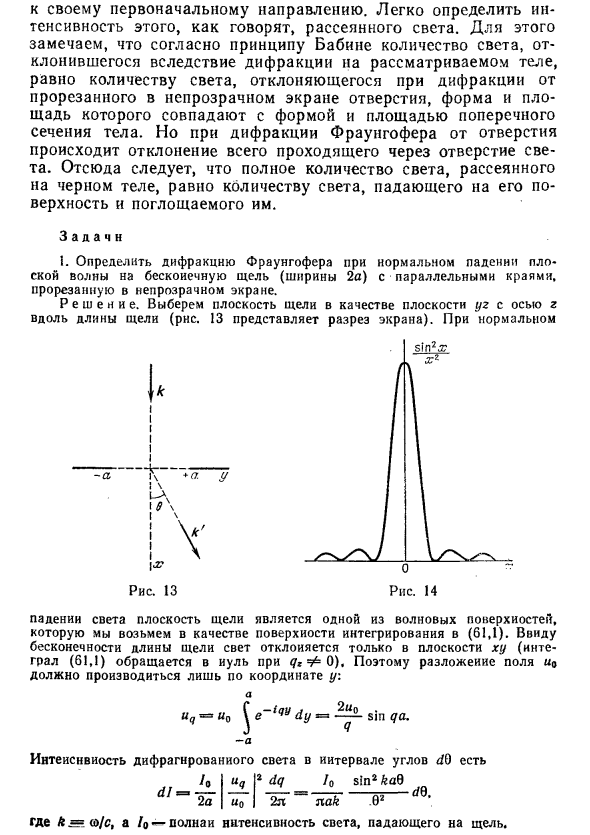
Однако во время дифракции Фраунгофера от отверстия весь свет, проходящий через отверстие, отклоняется. В результате общее количество света, рассеянного черным телом, равно количеству света, который падает на его поверхность и поглощается. Задача 1. Определить дифракцию Фраунгофера при нормальном падении на плоскость Волна бесконечной щели (ширина 2а) с параллельными ребрами, Слот на непрозрачном экране.
Решения. Выберите плоскость разреза как плоскость yz с осью z По длине щели (на рисунке 13 показана часть экрана). Для нормального падения света поверхность щели является одним из волновых фронтов, Принять это как поверхность Пометка (61.1).
Для бесконечной длины Щель освещается плоскостью XY (меж Чаша (61.1) исчезает с qzφ0. так Разложение поля r> 0 Координата y: и -iqy 1 : Chi dy = —— sm qa. Интенсивность рассеянного света в сечении Le угол d0 равен 2 I — O; к -А \ + <2 __L «\ \ * л = * ио дк 27G / о грех кав 7 г ак O2 х Рисунок 13 2 а Где k = uj / c и a / o — общая интенсивность света, падающего на щель.
Рисунок 3-14, dl / d0 как функция угла дифракции. Увеличение в направлении от 0 до 1 или другое направление увеличит интенсивность Быстро уменьшаться при высокой цене серии sin2 1 100 минут. Максима расколота в точке = = pj / ka (n — целое число), минимальное значение, Его сила исчезает. 2. То же самое для дифракции от решетки Плоский экран с множеством идентичных параллельных прорезей (ширина прорези 2a, непрозрачная ширина экрана между соседними прорезями 26, количество прорезей N).
Решения. Выберите плоскость решетки в качестве плоскости YZ оси Z Па Параллельная трещина. О дифракции существует только в плоскости ху, интегро (61.1) вводится 0 Рисунок 14 / 1— 2iNqd -2 iqd Где d = a + b, u’q — результат интегрирования в одну щель. Используйте результат задачи 1, чтобы получить: / sinNqd \ 2 / sinqa \ 2 ^ _ Iq / sinNk6d \ 2 sin2 cav V sintfd / V nn) Nilac ^ дл: ипа N7Gsin qd ‘, V V qam’) d q = -N irak, ^ sin kOd-) (/ O — общая интенсивность света, проходящего через все трещины).
При большом количестве слотов (N-L oo) это выражение может быть записано в другом формате. Если q = 7rn / d (где n — целое число), dl / dq имеет максимальное значение. Близко к такому максимуму (т. Е. Если qd = pm + e, r мало) dl = I0a [——— ——— * ~ dq. \ qa ‘7tNs Но Н-Уо формула sin2 Nx V lim ———— = d (x). N-T OO 7TNX Поэтому вблизи каждого максимального значения dI = Ioa (s m a y d {Ј) dЈ д ‘ка’
То есть максимальное значение имеет бесконечно малую ширину, а максимальное значение N-я максимальная интенсивность света t (p) _t d sin2 (n7ra / d) От 1 до 2 2 7 г 3. Определить распределение интенсивности в направлении ди Доля света, падающего в нормальном направлении на круглое отверстие Радиус а.
Решения. Цилиндрические координаты z, r, (p с осью z, Пройдите центр отверстия перпендикулярно его плоскости. Болит Дифракция симметрична относительно оси z и вектора q Он имеет только радиальную составляющую qr = q = sq.
Угол отсчета <р Интегрирование в направлении q и (61.1) вдоль плоскости отверстия, 2-7G uq-Uq J * J e ~ iqrcos (pr dip dr = 27tuo J Jo (qr) rdr, 0 0 0 Где Джо — функция Бесселя нулевого порядка. Используйте известную формулу / Jo (qr) rdr = —Ji (aq) Я д У нас отсюда 27ti0a,. Uq = ————— Q (61.4)
В зависимости от конечной интенсивности света, дифракция Телесный угол сделать элемент: дл = до 7g0 Где Iq — общая интенсивность света, падающего на отверстие. x) Для xΦ0 функция в левой части уравнения равна нулю, Формула известна из теории рядов Фурье, дх = / (0). Это указывает на то, что свойства этой функции действительно совпадают ^ Свойства функции (см. Примечание на стр. 103).
Смотрите также:
| Дифракция в физике | Запаздывающие потенциалы в физике |
| Дифракция Френеля | Потенциалы Лиенара—Вихерта |

