Оглавление:










Диффузия
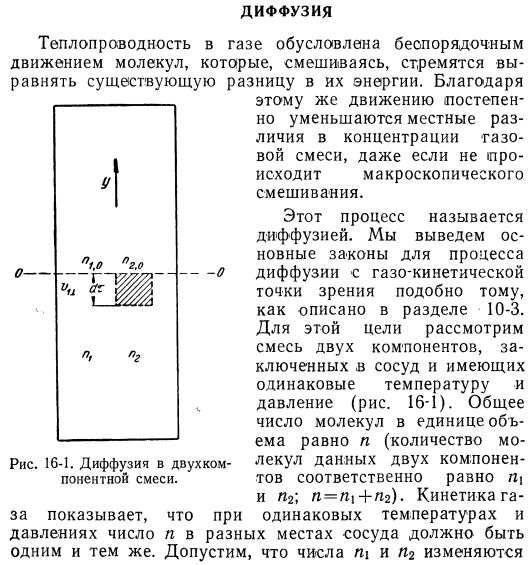
- Потому что теплопроводность газа нестабильна. При смешивании существующая разница в энергии имеет тенденцию выравниваться за счет движения молекул. Спасибо. Рис. 16-1. Диффузия в 2-компонентной смеси. Даже если макроскопического перемешивания не происходит, то такое же движение постепенно уменьшает локальную разницу в концентрации газовой смеси.
Этот процесс называется diffusion. As описанные в разделе 10-3, выводят основные законы диффузионных процессов с точки зрения газовой кинетики. Для этого рассмотрим смесь из 2 компонентов, которые помещены в контейнер и имеют одинаковую температуру и давление (Рис. 16-1). Общее число молекул в единице объема равно n (число молекул этих 2 компонентов равно p и n2 соответственно; n = ni + n2). Кинетика ха При одинаковой температуре и давлении указывают на то, что количество gy в разных местах сосуда должно быть одинаковым.
Оболочка, не допускающая теплообмен между системой и окружающей средой, называется адиабатической, а заключённая в такую оболочку система — теплоизолированной или адиабатически изолированной. Людмила Фирмаль
Предположим, что числа n и n₂ изменяются в «направлении y», n находится внизу, n находится в верхней части контейнера. В количестве 2 ингредиентов каждый ni. Рассмотрим плоскость 0-0, которая равна o и nu, о. Молекулы нерегулярного движения непрерывно пересекают эту плоскость. 0-0 все молекулы, входящие в малый объем элемента единицы базовой площади и высоты vₜ^ dx на плоскости, проходят через эту единицу площади 0-0 со временем dx, со средней скоростью (вверх по направлению).
Число молекул на единицу объема данного объемного элемента больше числа ni, ₀, вблизи плоскости o-0y, если эта плоскость совпадает с верхним дном. Это (сумма может быть выражена как: — Даже не знаю. О-ihdⁿjdyl Поскольку числитель подходит для mean среднее от плоскости 0 до расстояния/ x, где x-средний свободный путь и/ — номер порядка 1. In кроме того, можно описать следующие соотношения: vj = i’v y, где i ’представляет среднюю скорость молекулы типа 1, А i’ — число порядка 1.
Таким образом, число молекул 1y на единицу поверхности плоскости 0-o в единицу времени в вертикальном направлении будет равно: [«1. 0-i4dnₜ/ ды) ]. Число молекул, проходящих вниз по плоскости 0-0, равно следующему. ^»М + МОМО». И таким образом, результирующий поток молекул 0 через плоскость 0-0 1 будет: «、=-/ ^、1 ^、(16-1) Где ij = 2i’j-степень 1. Аналогично, результирующий поток числителя 0-0 через плоскость 2、 (16-2) Средний свободный путь зависит от размера как числителя/, так и числителя 2. Поэтому коэффициенты диффузии d₁ 1 к смеси 1 и 2 компонентов, ₁ 2, по формуле «、= −0, , ^、(16-3).
Коэффициенты диффузии П₂₁ газовой смеси 1 и 2 к 2 n₂= — dₜᵢ%. (16-4) Из Формулы n = nn — — nn и n = const、 днжды = — днжды. Чтобы поддерживать n = const во время процесса, общее число молекул на плоскости 0-0 должно быть равно нулю-| — n = 0). Следовательно, это d₂ = d₂ₗ. Коэффициент диффузии газа 1 совпадает с коэффициентом диффузии газа 2. В дальнейшем вы будете просто показывать их с буквой d. Цифровой коэффициент i [l. 278], коэффициент d практически не зависит от концентрации компонента в смеси, которая обратно пропорциональна давлению и увеличивается с температурой пропорционально 7′, b.
B имеет значение между 0, 5 и 1. 。 Р-9 содержит значения коэффициента диффузии для различных смесей. Обозначения n и n в формулах (16-3) и (16-4) также можно интерпретировать как единицу объема или грамм молекулы на единицу площади и времени соответственно. Для твердого и жидкого вещества коэффициент диффузии также определяется по формулам (16-3) и (16-4). Данные по таким коэффициентам и их зависимости от различных параметров значительно меньше, чем по данным газа. Уравнение диффузии также может быть выражено в терминах градиента концентрации.
Если умножить обе части формулы (16-3) на молекулярную массу al, то: (16-5) Где m-{массовый расход в единицу времени через единицу ПБ? Милость. ; pi-массовая концентрация компонентов v * » •>и a. Это уравнение часто называют законом Фика. Градиент парциального давления имеет следующий вид: Беспроводной ДПТ = Д-т• 1rxt ды Процесс диффузии, •показан на фиг. 16-1 называется эквимолярным anti-diffusion. In фактически, внутри контейнера наблюдается небольшое конвективное движение, как показано на рисунке 1. 16-1.
Это можно установить следующим образом: результирующий поток молекулы грамма через плоскость 0-0 равен суммарному потоку n2 молекулы грамма. Однако, когда молекулярная масса mi и М₂ отличается, оба массовых расхода не могут быть сбалансированы. Массовое течение происходит пока диффузия принимает place. To выведите уравнение совместного действия диффузии и конвекции при массопереносе, необходимо знать диффузионный поток молекул через плоскость, в которой конвекция не течет (конвекция ориентирована вдоль потока).
Чепмен и колинг вывели следующее уравнение для числа граммов молекул nₕ, которые проходят через единичную площадь на единичную плоскость со смесью из 2 компонентов, когда давление постоянно и отсутствует массовая сила, а температура изменяется локально. По этой формуле m — молекулярная масса смеси. Р-плотность смеси. Кт называется коэффициентом термодиффузии. 1. Эта формула показывает, что диффузия происходит в смеси, когда есть градиент температуры, но нет разницы в концентрации. Этот процесс называется термодиффузией.
Величина коэффициента температуропроводности равна、 1 Как правило, коэффициент температуропроводности называется количество ДКТ, а коэффициент кт называется температуропроводности. (Приблизительно.) Массовый расход происходит только тогда, когда разница температур велика. При обычном процессе массопереноса в технологии термодиффузии его можно игнорировать, и это делается с дальнейшим рассмотрением. Массовый расход может быть выражен очень просто массовым содержанием.
Умножим формулу (16-6) на afi и заменим молярное отношение Л1/п на массовое содержание о> 1, получим: v. (16-7) Термин, описывающий термодиффузию, здесь игнорируется. Это уравнение также может быть получено путем добавления конвективного массового потока к диффузионному потоку через плоскость 0-0 (см. Рис. 16-1). Сочетание диффузии и конвективного массопереноса, часто встречающееся в промышленных процессах, рассматривается на следующем простом примере. / Да2 1. 〜 1 / t2-0 iii! W1u> ’ u2w НПО Рисунок 16-2. In расчет диффузии водяного пара в воздухе. Налейте воду в нижнюю часть стеклянной трубки (рис. 16-2).
- Над открытым концом трубки движется воздух с определенным массовым содержанием водяного пара. Поэтому давление в трубке постоянно и равно внешнему давлению. Температура внутри трубки считается постоянной, а массовое содержание водяного пара снаружи трубки обычно отличается от массы на поверхности воды. Вообще говоря, парциальное давление водяного пара вне пробирки отличается от давления на поверхности воды. И это неудивительно, ведь парциальное давление пара на поверхности воды равно давлению насыщения, соответствующему температуре поверхности.
Поэтому массовое содержание предопределено. Согласно уравнению (16-7), существует градиент массовой концентрации и градиент диффузионного потока водяного пара в трубке. Так как массовое содержание водяного пара и воздуха равно 1, то градиент массового содержания пара соответствует градиенту массового содержания воздуха. Формула (16-7) также должна быть справедлива для воздуха, поэтому поток частиц воздуха должен быть одновременно с потоком частиц пара, но в противоположном направлении. Однако в нижней части трубки нет отверстий.
Это понятие в общем случае достаточно сложно определить строго, поэтому используется описательное определение, в котором термодинамической системой называется макроскопическая система. Людмила Фирмаль
Поэтому, чтобы компенсировать распространение воздуха в трубке, необходим восходящий ток через конвекцию. Пусть v-скорость конвекции. Количество пара в единицу времени, проходящего через поперечное сечение трубного блока этим потоком, равно pjtf. Таким образом, суммарная взвешенная скорость прохождения водяного пара через секцию 1-1 определяется по формуле: тело m₁₌= — др ^ — ф-п. О’. (16-8) То же самое уравнение относится и к потоку воздуха. Этот поток равен нулю, поэтому » получаем следующее выражение: ^ =- др ^ ’+p₂o=°. (16 ′ 9.).
Отсюда найдите значение скорости. Я пренебрегаю тобой, dw₂₂ ’ ды (16-10)- Массовое содержание воздуха может быть выражено как: o) ₂ = 1-wi、 dw₂__dwₓ Ди. ды ’ 1 теоретически давление пара на поверхности несколько ниже давления насыщения (существует поток частиц с поверхности, но разница очень мала и незначительна в практических расчетах). Между тем, тепло поглощается во время испарения. Часто из нижних слоев жидкости (она должна достигать surface. As в результате в верхнем слое вблизи поверхности жидкости наблюдается постоянный температурный градиент, а температура поверхности ниже средней температуры жидкости.
В результате вы получите: ОКР. 1-wₜdy (16-11) Массовый расход водяного пара через трубку по формуле (16-8) равен: dwdydy 1-dyp₂dy Для интегрирования этого уравнения удобно ввести парциальное давление. Использование уравнений Получать и dwₓ_r21 Дои ды ~~rir₂ » п » ды «условия ddp. » ««p₂* * Ж * ды ’ ______2_ П dp_i РЖ * П-ПЛ ды (16-12) (16-13) Это уравнение называется законом Стефана[l. 279]. Если площадь поперечного сечения трубки по y постоянна, то в этом случае t не зависит от y, можно интегрировать формулу (16-3). Когда вы изолируете переменную, вы видите следующее: — ма-Р’Т ды. П — — — пи д р у.
И если мы интегрируем с интервалами r / = 0 и y = 1>, то это выглядит так: И отсюда (16-14) Используя это уравнение, можно рассчитать удельный расход водяного пара, используя известный коэффициент диффузии парциального давления на поверхности воды и при открытии трубы. И, наоборот, вы можете решить Значение измеренного парциального давления и коэффициента диффузии массы испаренной воды за 1 час. Если разница между парциальными давлениями невелика по сравнению с полным давлением, то вместо формулы (16-14) можно использовать более простую формулу. Эта формула полностью аналогична формуле для определения теплового потока через плоскую стенку за счет теплопроводности (1-7).
Закон Стефана, который выражается в уравнении (16-13), при незначительной разнице парциального давления превращается в закон Фика, который описывается в уравнении (16-5). Последнее по форме аналогично общему уравнению теплопроводности (2-2). Поскольку парциальное давление изменяется более широко, формуле (16-14) можно придать вид, аналогичный формуле (16-15), следующим образом: d p p pp w * i’wp₂w-p₂ p2w p2 (16-16) Где p₂ᵣₙ-среднее логарифмическое давление, которое можно определить с помощью таблицы. 1-2. ; p1p₂, n-коэффициент увеличения массового расхода при диффузии process. It показано на рисунке. 16-2, чем при расчете по формуле (16-15).
Ранее были сделаны расчеты о случае, когда вода испаряется в воздух, чтобы связать его с конкретным случаем. Однако они могут быть применены в случае взаимной диффузии любых 2 газов. Формула (16-8) и соответствующий 2-й газ обычно действительны! В общем случае » уравнение (16-13) справедливо только на поверхностях, где один из этих 2 газов не проникает, и в изотермических условиях, а применение решения (16-14) ограничивается случаем 1d течения. Все процессы испарения, конденсации и сублимации от поверхности к газу соответствуют условиям полупроницаемой поверхности.
Для обоих компонентов могут существовать массовые расходы. Например, когда твердая углеродная поверхность сгорает, кислород будет диффундировать к поверхности, а окись углерода или диоксид углерода, образующиеся при горении, будут диффундировать Он финансируется за счет ie. In в этом случае уравнение (16-10) следует заменить уравнением, учитывающим тот факт, что отношение скоростей двух масс на поверхности задается стехиометрическим соотношением, описывающим процесс горения.
Интересно отметить, что перенос энтальпии также связан с диффузионным процессом в j *изотермическом field. In пример показан на рисунке, когда вода из 16-27 паров диффундирует, поток энтальпии в единицу времени равен единице поверхности Даже на поверхности, расположенной в Газе таким образом, что нет чистого массового потока (mx = gp2) *, если есть еще поток энтальпии, а также разность температур, равная mi (cpi-cp2) ; что пот»тепло на единицу площади—тепло в единицу времени»находится в том же потоке, что и Вена. + м> (с, , Л-cₚjt-⁽1⁶1⁷⁾ направление y предполагается перпендикулярным плоскости.
На рисунке 1 показан тепловой поток в единицу времени на единицу поверхности через плоскость 1-1 равную 16-2, Второзаконие| 〜 7 = — * — ay + micpit, если температура в трубке не совпадает. Из уравнений (16-8) и (16-11), соотношения от, = — + p, t> = = ₽ (! В +₽ » = по И л / т Пример 16-1. В нижней части вертикальной трубы с поперечным сечением 5 см2 находится вода. Расстояние от поверхности воды до открытого конца трубки составляет 6, 37 см, и полностью сухой воздух движется по открытому концу трубки. Температура трубки постоянна и равна 30, 8°c. by взвешивая, определяют, что вода испаряется со скоростью 2, 542 ИО-⁵кг / h. It необходимо определить коэффициент диффузии водяного пара.
Массовая скорость 2, 542-10 — ⁵ ТХ = — $ 10_₄— = 0. 51 «10- *1kg1m2-Н. * В дополнение к эффекту Дюфо, диффузия передает энергию только молекулам с внутренними степенями свободы 1 p i p p * _ и v. Л н Согласно данным таблицы, давление насыщения воды rtapa при 30, 8°c/? ₁a, = 452 кг {м2. Газовая постоянная водяного пара определяется молекулярной массой l4g = 18, 016 и универсальной газовой постоянной 91 = 0, 848 до Г М / Град моль. 91 _ 0. 848 18. 02. = 47, 1 КГМ / град кг.
Решая уравнение (16-14) относительно d, получим: ntjlryt_________ Д / > В[/> / (/> — В _0. 51-10-«. 47. 1-0. 064 (273 + 30. 8)」 10, 000-л / ч 1, 000•2, 31 г пробежка _ 452 Для получения достоверного результата необходимо использовать трубки малого диаметра. В противном случае температура поверхности воды может быть значительно ниже температуры окружающей среды, и кроме того, воздух вблизи поверхности легче воздуха на открытом конце трубки, потому что сухой воздух тяжелее влаги, что может вызвать естественную конвекцию.
Смотрите также:

