Дифференцируемость и полный дифференциал функции
Пусть функция 
определена в некоторой окрестности точки 
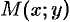. Составим полное приращение функции в точке 
:
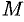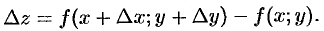
Функция называется дифференцируемой в точке 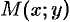, если ее полное приращение в этой точке можно представить в виде
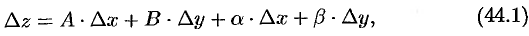
где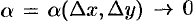 
и 
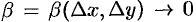при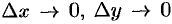 
. Сумма первых двух слагаемых в равенстве (44.1) представляет собой главную часть приращения функции.
Главная часть приращение функции , линейная относительно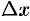 
и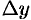 
, называется полным дифференциалом этой функции и обозначается символом 
:
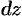Выражения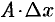 
и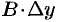 
называют частными дифференциалами. Для независимых переменных 
и 
полагают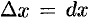 
и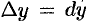 
. Поэтому равенство (44.2) можно переписать в виде
Теорема 44.2 (необходимое условие дифференцируемости функции). Если функция дифференцируема в точке 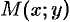, то она непрерывна в этой точке, имеет в ней частные производные 
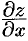и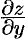 
, причем 
.
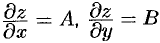Так как функция дифференцируема в точке 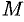, то имеет место равенство (44.1). Отсюда вытекает, что 
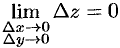. Это означает, что функция непрерывна в точке 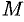. Положив 
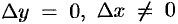в равенстве (44.1), получим: 
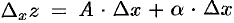. Отсюда находим 
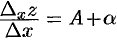. Переходя к пределу при 
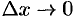, получим 
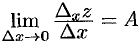, т. е. 
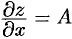. Таким образом, в точке 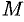существует частная производная 
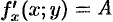. Аналогично доказывается, что в точке 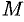существует частная производная 
.
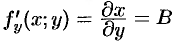Равенство (44.1) можно записать в виде
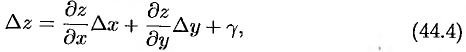
где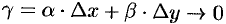 
при .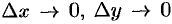
Отметим, что обратное утверждение не верно, т. е. из непрерывности функции или существования частных производных не следует дифференцируемость функции. Так, непрерывная функция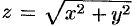 
не дифференцируема в точке (0;0).
Как следствие теоремы получаем формулу для вычисления полного дифференциала. Формула (44.3) принимает вид:
или
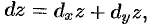
где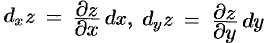 
— частные дифференциалы функции .
Теорема 44.3 (достаточное условие дифференцируемости функции). Если функция имеет непрерывные частные производные 
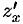и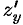 
в точке 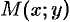, то она дифференцируема в этой точке и ее полный дифференциал выражается формулой (44.5).
Примем теорему без доказательства.
Отметим, что для функции 
одной переменной существование производной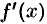 
в точке является необходимым и достаточным условием ее дифференцируемости в этой точке.
Чтобы функция была дифференцируема в точке, необходимо, чтобы она имела в ней частные производные, и достаточно, чтобы она имела в точке непрерывные частные производные.
Арифметические свойства и правила исчисления дифференциалов функции одной переменной сохраняются и для дифференциалов функции двух (и большего числа) переменных.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Геометрический смысл частных производных функции двух переменных |
| Частные производные высших порядков |
| Применение полного дифференциала к приближенным вычислениям |
| Дифференциалы высших порядков |
