Оглавление:
Дифференцирование неявно заданной функций
1) Функция независимой переменной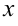 
называется неявной, если она определяется из неразрешенного уравнения, связывающего аргумент и функцию 
: 
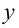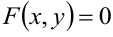. Часто разрешить это уравнение невозможно или нецелесообразно. При этом можно определить производную функции, дифференцируя обе части равенства по 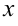, помня, что 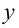есть функция от .
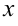Пример №1.
Определить производную функции, заданной неявно
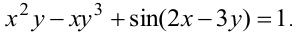
Решение:
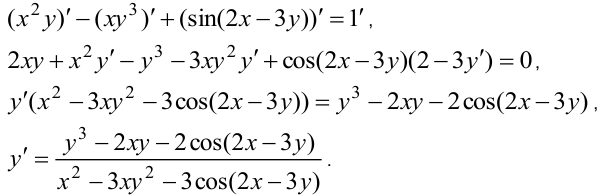
Как видим, производная выражается явно относительно аргумента 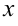и функции .
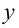Дифференцирование логарифмических заданных функций
2) Для дифференцирования функции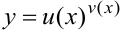 
нельзя непосредственно применить ни одно из правил дифференцирования или пункт таблицы производных, так как и основание и показатель степени — функции независимой переменной. Функция называется показательно — степенной или сложной показательной.
Дифференцирование возможно, если вначале определить производную натурального логарифма функции. Определяем натуральный логарифм показательно — степенной функции: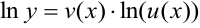 
. Теперь
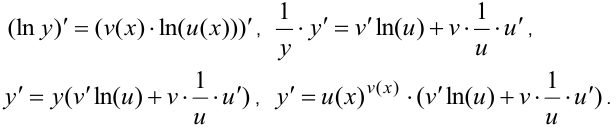
Производная от натурального логарифма функции называется также логарифмической производной.
Пример №2.
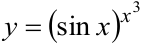
Решение:
Логарифмируем левую и правую части по основанию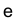 
:
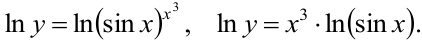
Теперь дифференцируем равенство, учитывая, что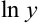 
— сложная функция, так как 
.
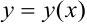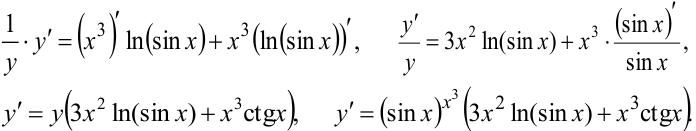
Дифференцирование параметрически заданных функций
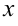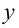3) Координаты точки на плоскости и могут быть заданы в зависимости от некоторой третьей переменной, например, времени 
:
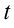Эта переменная 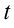является параметром. Когда 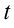изменяется, то точка на плоскости описывает некоторую линию 
. Эта линия задана в параметрическом виде. Например, уравнение окружности с центром в начале координат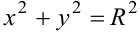 
в параметрическом виде задается уравнениями
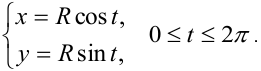
В случае с уравнением окружности параметр 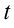— угол между положительным направлением оси 
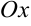и радиус — вектором движущейся по окружности точки.
Если функция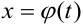 
имеет обратную функцию 
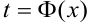, то 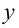является функцией от : 
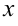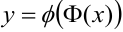. Таким образом, уравнения (5.9) определяют 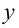как функцию от 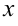и говорят, что функция 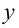задана параметрически.
Пусть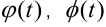 
— дифференцируемые функции параметра 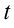, причем 
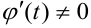. Как всякие дифференцируемые функции они непрерывные. В силу этого при 
.
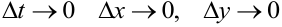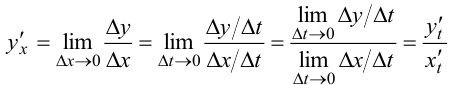. Таким образом,
Пример №3.
Определить производную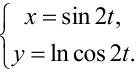 
Решение:
Используя формулу (5.10), найдём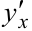 
для функции, заданной параметрически. Дифференцируем по 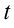переменные 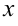и :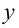
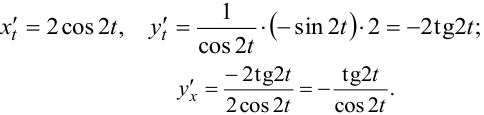
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
