Оглавление:
Неявно заданная функция
Если функция задана уравнением 
, разрешенным относительно 
, то функция задана в явном виде (явная функция).
Под неявным заданием функции понимают задание функции в виде уравнения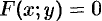 
, не разрешенного относительно .
Всякую явно заданную функцию
можно записать как неявно заданную уравнением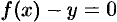 
, но не наоборот.
Не всегда легко, а иногда и невозможно разрешить уравнение относительно (например,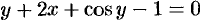 
или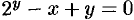 
).
Если неявная функция задана уравнением 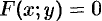, то для нахождения производной от по 
нет необходимости разрешать уравнение относительно : достаточно продифференцировать это уравнение по , рассматривая при этом у как функцию , и полученное затем уравнение разрешить относительно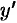 
.
Производная неявной функции выражается через аргумент
и функцию .
Пример №21.1.
Найти производную функции , заданную уравнением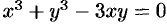 
.
Решение:
Функция задана неявно. Дифференцируем по равенство 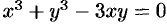. Из полученного соотношения
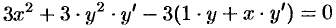
следует, что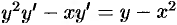 
, т. е. 
.
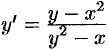На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Таблица производных. Правила дифференцирования. Формулы дифференцирования |
| Таблица дифференциалов |
| Дифференцирование функции, заданной параметрически |
| Логарифмическое дифференцирование функций |
