Оглавление:
Дифференцирование функции комплексного переменного. Условия Эилера-Даламбера
Пусть однозначная функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  , включая и саму точку. Тогда предел
, включая и саму точку. Тогда предел
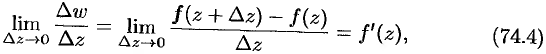
если он существует, называется производной функции  в точке
в точке  , а функция
, а функция  называется дифференцируемой в точке
называется дифференцируемой в точке  .
.
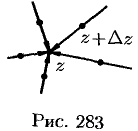
Подчеркнем, что в равенстве (74.4) 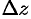 любым образом стремится к нулю, т. е. точка
любым образом стремится к нулю, т. е. точка 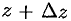 может приближаться к точке
может приближаться к точке  но любому из бесконечного множества различных направлений (см. рис. 283) (в аналогичной ситуации для функции одного действительного переменного точка
но любому из бесконечного множества различных направлений (см. рис. 283) (в аналогичной ситуации для функции одного действительного переменного точка 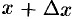 ; приближается к точке
; приближается к точке  лишь по двум направлениям: слева и справа).
лишь по двум направлениям: слева и справа).
Из дифференцируемости функции  в некоторой точке
в некоторой точке  следует ее непрерывность в этой точке (отношение
следует ее непрерывность в этой точке (отношение 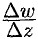 при
при 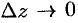 может стремиться к конечному пределу
может стремиться к конечному пределу 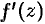 лишь при условии, что и
лишь при условии, что и 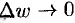 ). Обратное утверждение не имеет места.
). Обратное утверждение не имеет места.
При каких условиях функция  будет дифференцируемой в данной точке?
будет дифференцируемой в данной точке?
Теорема 74.1. Если функция 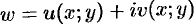 определена в некоторой окрестности точки
определена в некоторой окрестности точки 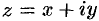 , причем в этой точке действительные функции
, причем в этой точке действительные функции 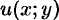 и
и 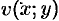 дифференцируемы, то для дифференцируемости функции
дифференцируемы, то для дифференцируемости функции  в точке
в точке  необходимо и достаточно, чтобы в этой точке выполнялись равенства
необходимо и достаточно, чтобы в этой точке выполнялись равенства
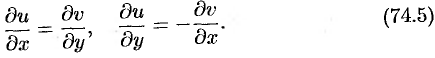
Равенства (74.5) называются условиями Эйлера-Даламбера (или условиями Коши-Римана).
Необходимость
Пусть функция  дифференцируема в точке
дифференцируема в точке  , тогда предел (74.4) существует и не зависит от пути, по которому
, тогда предел (74.4) существует и не зависит от пути, по которому 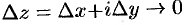 . Можно считать, что точка
. Можно считать, что точка 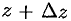 приближается к точке
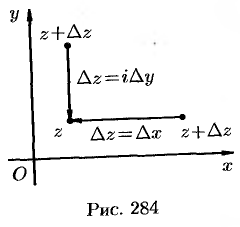
приближается к точке  по прямой, параллельной действительной оси (оси
по прямой, параллельной действительной оси (оси  ), т. е.
), т. е. 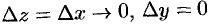 (рис. 284). Тогда
(рис. 284). Тогда
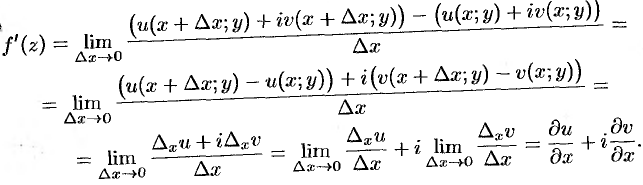
Если же точка 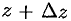 приближается к точке
приближается к точке  по прямой, параллельной мнимой оси (оси
по прямой, параллельной мнимой оси (оси 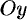 ), то
), то 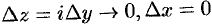 . В этом случае
. В этом случае
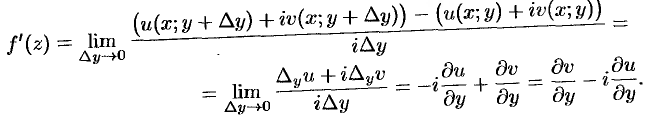
Сравнив найденные пределы, получим 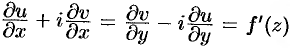 .
.
Отсюда следует: 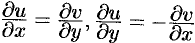 .
.
Достаточность
Пусть теперь условия (74.5) выполняются. Докажем, что функция  дифференцируема.
дифференцируема.
Так как функции 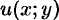 и
и 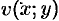 дифференцируемы в точке
дифференцируемы в точке 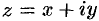 , то их полные приращения можно представить (см. (44.4)) в виде
, то их полные приращения можно представить (см. (44.4)) в виде 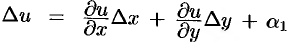 ,
, 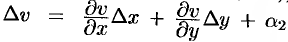 , где
, где 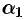 и
и 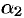 — бесконечно малые более высокого порядка, чем
— бесконечно малые более высокого порядка, чем 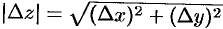 . Тогда
. Тогда
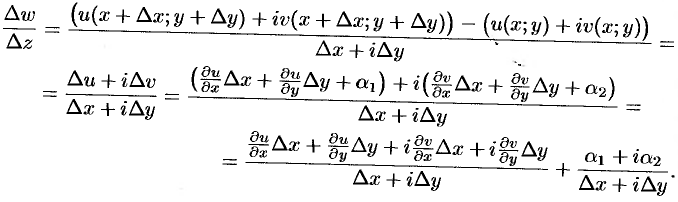
Заменяя в числителе правой части 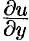 на
на 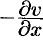 ,
, 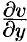 на
на 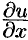 согласно
согласно
условиям (74.5), получаем:
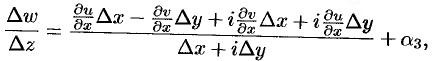
где
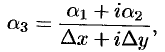
т.е.
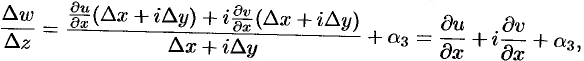
а 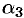 — бесконечно малая высшего порядка относительно
— бесконечно малая высшего порядка относительно 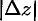 . Отсюда следует, что
. Отсюда следует, что 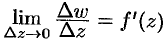 существует. При этом
существует. При этом 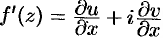 .
.
С учетом условий Эйлера-Даламбера (74.5) производную дифференцируемой функции  можно находить по формулам
можно находить по формулам
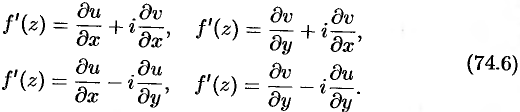
Правила дифференцирования функций действительного переменного справедливы и для функций комплексного переменного, дифференцируемых в точке  . Это означает, что если
. Это означает, что если 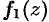 и
и 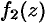 дифференцируемы в некоторой точке
дифференцируемы в некоторой точке  комплексной плоскости, то верно следующее:
комплексной плоскости, то верно следующее:
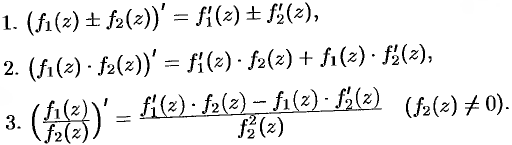
 Если
Если 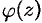 дифференцируема в точке
дифференцируема в точке  , a
, a 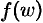 дифференцируема в точке
дифференцируема в точке 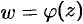 , то
, то 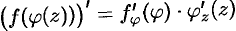 .
.
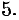 Если в некоторой точке
Если в некоторой точке  функция
функция  дифференцируема и существует функция
дифференцируема и существует функция 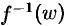 , дифференцируемая в точке
, дифференцируемая в точке  , причем
, причем 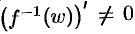 , то
, то 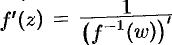 , где
, где 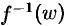 — функция, обратная функции
— функция, обратная функции  .
.
Приведем без доказательства теорему о дифференцируемости основных элементарных функций комплексного переменного: функции 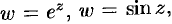
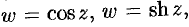
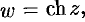
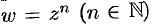 дифференцируемы в любой точке комплексной плоскости; функции
дифференцируемы в любой точке комплексной плоскости; функции 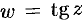 и
и 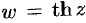 также дифференцируемы в любой точке плоскости, кроме точек
также дифференцируемы в любой точке плоскости, кроме точек 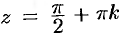 и
и 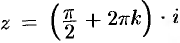 (
(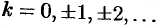 ) соответственно; для функций
) соответственно; для функций 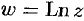 ,
, 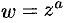 в окрестности каждой точки
в окрестности каждой точки 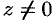 можно выделить однозначную ветвь, которая является дифференцируемой в точке
можно выделить однозначную ветвь, которая является дифференцируемой в точке  функцией.
функцией.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Ротор векторного поля. Формула Стокса |
| Свойства основных классов векторных полей |
| Аналитическая функция тфкп |
| Геометрический смысл модуля и аргумента производной |

