Оглавление:
Дифференциалы высших порядков
Пусть  дифференцируемая функция, а ее аргумент
дифференцируемая функция, а ее аргумент  — независимая переменная. Тогда ее первый дифференциал
— независимая переменная. Тогда ее первый дифференциал 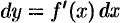 есть также функция
есть также функция  ; можно найти дифференциал этой функции.
; можно найти дифференциал этой функции.
Дифференциал от дифференциала функции  называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается
называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается 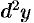 или
или 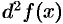 .
.
Итак, по определению 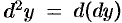 . Найдем выражение второго дифференциала функции
. Найдем выражение второго дифференциала функции  .
.
Так как 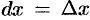 не зависит от
не зависит от  , то при дифференцировании считаем
, то при дифференцировании считаем 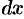 постоянным:
постоянным:
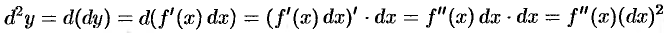
т. е.

Здесь 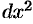 обозначает
обозначает 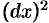 .
.
Аналогично определяется и находится дифференциал третьего по-
рядка:
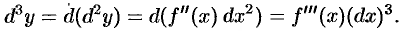
И, вообще, дифференциал 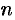 -го порядка есть дифференциал от дифференциала (
-го порядка есть дифференциал от дифференциала (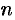 -1)-го порядка:
-1)-го порядка: 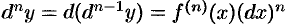 .
.
Отсюда находим, что 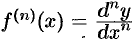 . В частности, при
. В частности, при 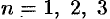 соответственно получаем:
соответственно получаем:
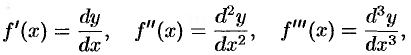
т. е. производную функции можно рассматривать как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.
Отметим, что все приведенные выше формулы справедливы только, если  — независимая переменная. Если же функцию
— независимая переменная. Если же функцию  , где
, где  — функция от какой-то другой независимой переменной, то дифференциалы второго и выше порядков не обладают свойством инвариантности формы и вычисляются по другим формулам. Покажем это на примере дифференциала второго порядка.
— функция от какой-то другой независимой переменной, то дифференциалы второго и выше порядков не обладают свойством инвариантности формы и вычисляются по другим формулам. Покажем это на примере дифференциала второго порядка.
Используя формулу дифференциала произведения 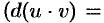
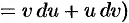 , получаем:
, получаем:
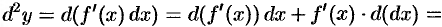
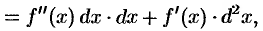
т.е.
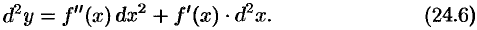
Сравнивая формулы (24.5) и (24.6), убеждаемся, что в случае сложной функции формула дифференциала второго порядка изменяется: появляется второе слагаемое 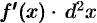 .
.
Ясно, что если  — независимая переменная, то
— независимая переменная, то
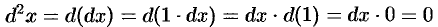
и формула (24.6) переходит в формулу (24.5).
Пример №24.6.
Найти 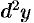 , если
, если 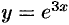 и
и  — независимая переменная.
— независимая переменная.
Решение:
Так как 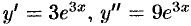 , то по формуле (24.5) имеем
, то по формуле (24.5) имеем
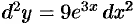 .
.
Дополнительный пример №24.7.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Производные высших порядков от функций, заданных параметрически |
| Применение дифференциала к приближенным вычислениям |
| Теоремы о дифференцируемых функциях |
| Возрастание и убывание функций |

