Дифференциалы высших порядков
Введем понятие дифференциала высшего порядка. Полный дифференциал функции (формула (44.5)) называют также дифференциалом первого порядка.
Пусть функция 
имеет непрерывные частные производные второго порядка. Дифференциал второго порядка определяется по формуле 
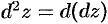. Найдем его:
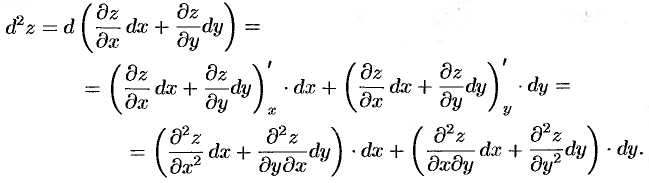
Отсюда: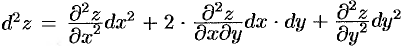 
. Символически это записывается так:
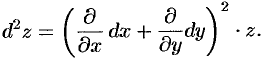
Аналогично можно получить формулу для дифференциала третьего порядка:
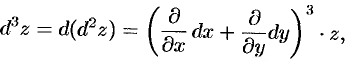
где
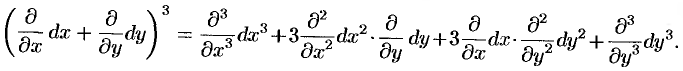
Методом математической индукции можно показать, что
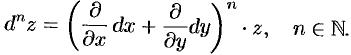
Отметим, что полученные формулы справедливы лишь в случае, когда переменные 
и 
функции являются независимыми.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Дифференцируемость и полный дифференциал функции |
| Применение полного дифференциала к приближенным вычислениям |
| Производная сложной функции |
| Инвариантность формы полного дифференциала |
