Оглавление:
Дифференциальные уравнения с разделяющимися переменными
В общем виде дифференциальное уравнение с разделяющимися переменными записывается следующим образом:
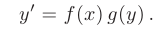
Для нахождения общего решения данного дифференциального уравнения используем следующий алгоритм:
- Запишем производную искомой функции в виде отношения дифференциалов
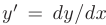 . В таком случае исходное уравнение примет вид
. В таком случае исходное уравнение примет вид
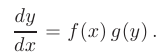
- Умножим обе части уравнения на
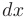 . В результате получим
. В результате получим
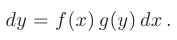
- Чтобы переменные
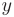 и
и 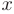 были разделены знаком равенства, разделим обе части уравнения на функцию
были разделены знаком равенства, разделим обе части уравнения на функцию 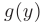 :
:
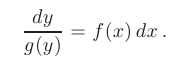
- Проинтегрировав левую и правую части полученного равенства по переменным
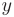 и
и 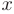 , получим общий интеграл дифференциального уравнения
, получим общий интеграл дифференциального уравнения
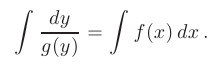
- Наконец, выразив
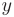 через
через 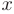 и
и 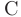 придем к общему решению дифференциального уравнения с разделяющимися переменными.
придем к общему решению дифференциального уравнения с разделяющимися переменными.
Пример:
Найти общее решение дифференциального уравнения с разделяющимися переменными
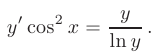
► Полагая
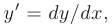
запишем данное уравнение в виде
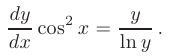
Произведем разделение переменных. Для этого умножим обе части уравнения на 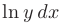 , а затем разделим их на
, а затем разделим их на 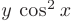 . После сокращения дробей получим
. После сокращения дробей получим
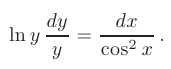
Теперь проинтегрируем обе части полученного уравнения:
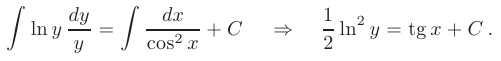
Последнее выражение представляет собой общий интеграл дифференциального уравнения. Выразив из него у получим искомое общее решение дифференциального уравнения с разделяющимися переменными:
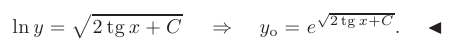
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:

