Оглавление:
Наиболее простым дифференциальным уравнением первого порядка является уравнение вида: 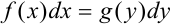 . В нем в левой части стоит функция
. В нем в левой части стоит функция 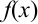 , зависящая только от переменной
, зависящая только от переменной 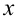 , а в правой — функция
, а в правой — функция 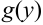 , зависящая только от переменной
, зависящая только от переменной 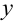 . Такое дифференциальное уравнение называют уравнением с разделенными переменными.
. Такое дифференциальное уравнение называют уравнением с разделенными переменными.
Для нахождения решения такого уравнения достаточно взять интеграл от обеих частей: 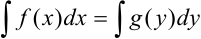 .
.
Пример №38.4.
Найдите решение дифференциального уравнения: 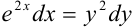 .
.
Решение:
Данное дифференциальное уравнение представляет собой уравнение с разделенными переменными. Проинтегрируем обе части уравнения:
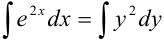 . Тогда
. Тогда
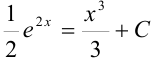 — общее решение дифференциального уравнения
— общее решение дифференциального уравнения 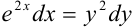 .
.
Ответ: 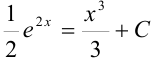 .
.
Если дифференциальное уравнение путем преобразований можно привести к виду 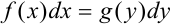 , то оно называется дифференциальным уравнением с разделяющимися переменными.
, то оно называется дифференциальным уравнением с разделяющимися переменными.
Для решения такого уравнения необходимо:
- Если в уравнении встречается
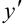 , то представить его как
, то представить его как 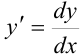 .
. - Произвести разделение переменных (в одной части при
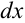 собрать выражения, содержащие только переменную
собрать выражения, содержащие только переменную 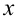 ; в другой части при
; в другой части при 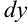 собрать выражения, содержащие только переменную
собрать выражения, содержащие только переменную 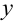 ).
). - Почленно проинтегрировать уравнение с разделенными переменными.
Пример №38.5.
Найдите решение дифференциального уравнения: 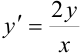 .
.
Решение:
Данное уравнение — дифференциальное уравнение с разделяющимися переменными. Представим 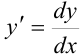 , тогда
, тогда 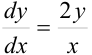 или
или 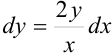 .
.
Будем собирать множители с 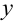 в левой части, с
в левой части, с 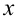 — в правой:
— в правой: 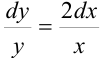 .
.
Интегрируя обе части, получим: 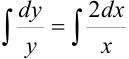 или
или 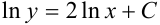 — общее решение.
— общее решение.
Ответ: 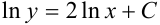 .
.
Замечание. Иногда при нахождении решения дифференциального уравнения, каждое слагаемое которого представляет собой натуральный логарифм, в качестве константы можно выбирать 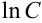 . Такую операцию можно было бы произвести в примере 38.5. Тогда общее решение дифференциального уравнения имело бы вид:
. Такую операцию можно было бы произвести в примере 38.5. Тогда общее решение дифференциального уравнения имело бы вид: 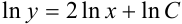 . Применим свойства логарифма:
. Применим свойства логарифма: 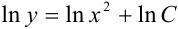 или
или 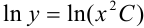 . Откуда можно заключить, что
. Откуда можно заключить, что 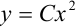 . Этот прием особенно эффективен при решении задачи Коши.
. Этот прием особенно эффективен при решении задачи Коши.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие дифференциального уравнения. |
| Простейшие дифференциальные уравнения первого порядка. |
| Приложение дифференциальных уравнений. |
| Понятие однородного дифференциального уравнения первого порядка. |

