Оглавление:
Дифференциальные уравнения плоского движения твердого тела
Уравнения плоского движения твердого тела (см. § 60) имеют вид:
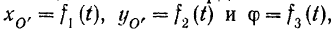
где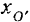 
и 
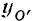— координаты произвольного полюса 
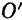относительно неподвижной системы координат и 
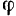— угол поворота тела вокруг выбранного полюса.
Уравнения плоского движения твердого тела получаются наиболее просто, если за полюс принять центр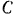 
масс тела.
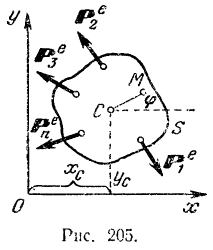
Рассечем мысленно тело плоскостью, параллельной данной неподвижной плоскости и проходящей через центр 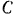масс тела. Положение этого сечения 
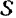(рис. 205), а следовательно, и положение самого тела, будет определяться координатами 
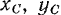центра 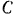масс тела и углом 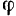поворота тела вокруг оси, проходящей через центр 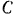масс тела и перпендикулярной даyной неподвижной плоскости. Пусть на тело действуют внешние силы
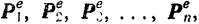
лежащие в плоскости сечения .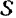
По теореме о движении центра масс (§ 89) имеем:
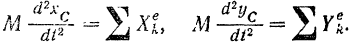
Так как по доказанному выше (§ 94) теорема об изменении кинетического момента системы приложима к движению системы относительно оси, проходящей через центр масс и движущейся поступательно вместе с центром масс, в той же форме, что и для неподвижной оси, то согласно уравнению (182), выведенному на основании этой теоремы, будем иметь:
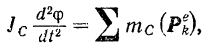
где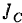 
— момент инерции тела относительно оси, проходящей через центр масс тела и перпендикулярной неподвижной плоскости, 
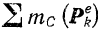— сумма моментов всех внешних сил, действующих на тело, относительно той же оси.
Таким образом, дифференциальными уравнениями плоского движения тела будут:
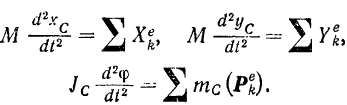
С помощью уравнений (183) по известным внешним силам, действующим на тело, можно определить закон его движения и, наоборот, зная закон движения тела, определить силы, действующие на тело.
Пример задачи:
Барабан однородной круглой катушки обмотан нитью так (рис. 206), что концы ее расходятся в противоположные стороны и натягиваются постоянными горизонтальными силам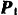и 
и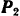 
. Вес катушки 
, радиус катушки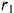 
, радиус ее барабана 
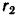и момент инерции катушки относительно оси симметрии, проходящей через центр 
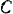тяжести катушки, 
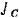Определить ускорение 
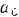оси 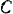катушки, предполагая, что она катится по горизонтальной плоскости без скольжения.
Решение:
На катушку действуют внешние силы: , 
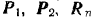—- нормальная реакция плоскости и 
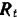— сила трения катушки о горизонтальную плоскость. Очевидно, что под действием этих сил все точки катушки будут двигаться в плоскостях, параллельных неподвижной вертикальной плоскости 
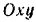(рис. 206). Дифференциальные уравнения плоского движения катушки имеют вид:
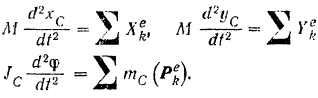
Проектируя все внешние силы, приложенные к катушке, на выбранные координатные оси и находя сумму моментов этих сил относительно оси, перпендикулярной к плоскости рисунка и проходящей через точку 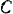колеса, будем иметь:
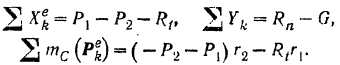
При движении катушки
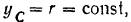
поэтому
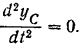
Подставляя найденные значения (II) и (III) в уравнения (I) получим:
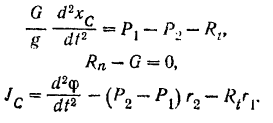
Из уравнения (V) находим
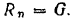
Так как точка движется параллельно оси 
, то алгебраическое значение ускорения этой точки равно
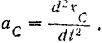
Для его определения из уравнения (IV) нужно знать величину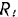 
. Так как катушка катится без скольжения, то нельзя считать
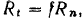
т. е. равной максимальной величине силы трения. Это обязательно имеет место лишь в случае, когда катушка скользит по плоскости. При отсутствии же скольжения
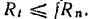
Из уравнения (VI) имеем:
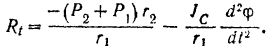
При качении катушки без скольжения мгновенным центром ее скоростей является точка касания колеса с плоскостью. Следовательно,
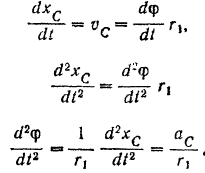
Подставляя значение (VIII) в равенство (VII), получаем:
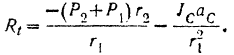
Подставляя значение (IX) в уравнение (IV), будем иметь:
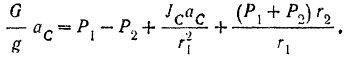
Решая последнее уравнение, находим искомое значение ускорения оси колеса:
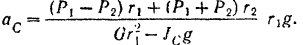
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
