Дифференциальным уравнением называется уравнение, связывающее независимую переменную 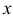 , искомую функцию
, искомую функцию 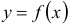 и ее производные у
и ее производные у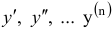 .
.
Символически дифференциальное уравнение можно написать так:
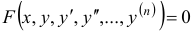 , или
, или 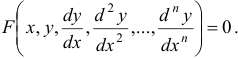
Неизвестной здесь является функция 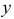 , входящая под знак производных (или дифференциалов).
, входящая под знак производных (или дифференциалов).
Если искомая функция 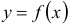 есть функция одной независимой переменной, то дифференциальное уравнение называется обыкновенным.
есть функция одной независимой переменной, то дифференциальное уравнение называется обыкновенным.
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
Например, уравнение 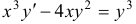 есть уравнение первого порядка, а уравнение
есть уравнение первого порядка, а уравнение 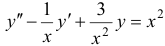 — уравнение второго порядка.
— уравнение второго порядка.
Решением дифференциального уравнения называется всякая функция 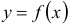 , обращающая это уравнение в тождество.
, обращающая это уравнение в тождество.
Решение 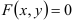 , заданное в неявном виде, называется интегралом дифференциального уравнения.
, заданное в неявном виде, называется интегралом дифференциального уравнения.
График дифференциального уравнения называется интегральной кривой.
Общим решением дифференциального уравнения 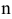 -го порядка называется функция
-го порядка называется функция 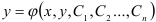 , зависящая от
, зависящая от 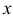 и
и 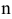 произвольных независимых постоянных
произвольных независимых постоянных 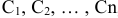 , обращающая это уравнение в тождество.
, обращающая это уравнение в тождество.
Общее решение, заданное в неявном виде 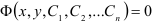 называется общим интегралом.
называется общим интегралом.
Частным решением дифференциального уравнения называется решение, которое получается из общего, если придать определенные значения произвольным постоянным.
Частным интегралом называется интеграл, полученный из общего, если придать определенные значения произвольным постоянным.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Интегрирование путем подстановки: определение и примеры с решением |
| Определенный интеграл |
| Уравнения с разделяющимися переменными |
| Однородные уравнения первого порядка |
