Дифференциальные уравнения движения материальной точки в декартовых координатах
Задачи динамики точки решаются с помощью уравнений, устанавливающих зависимости между координатами движущейся точки и действующими на псе силами. Найдем эти уравнения.
Из кинематики мы знаем, что движение точки вполне определенно, если известны законы, по которым изменяются со временем координаты 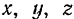 этой точки относительно какой-либо неподвижной (инерциальной) системы отсчета.
этой точки относительно какой-либо неподвижной (инерциальной) системы отсчета.
Таким образом, движение точки известно, если известны ее уравнения движения 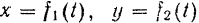 и
и 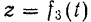 .
.
Силу 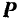 действующую на точку, мы также можем считать известной, если известны ее проекции
действующую на точку, мы также можем считать известной, если известны ее проекции 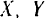 и
и 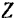 на координатные осн.
на координатные осн.
Пусть материальная точка 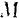 массы
массы 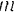 под действием приложенной к ней силы
под действием приложенной к ней силы 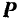 движется относительно некоторой неподвижной системы координатных осей но какой-либо траектории
движется относительно некоторой неподвижной системы координатных осей но какой-либо траектории 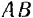 (рис. 102).
(рис. 102).
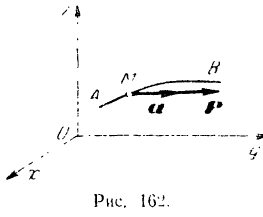
Зависимость между ускорением 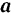 точки и приложенной к ней силой
точки и приложенной к ней силой 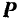 выражается, как мы знаем, основным уравнением динамики точки (106):
выражается, как мы знаем, основным уравнением динамики точки (106):
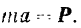
Спроектируем это векторное равенство ни координатные оси.
Так как проекция произведения вектора на скаляр равна произведению проекции этого вектора на данным скаляр, то мы получим:
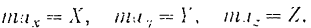
Но как известно из кинематики (§ -16). проекции ускорения па координации оси равны вторым производным от соответствующих координат движущейся точки по времени:
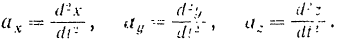
Подставляя эти значения в предыдущие уравнения, получим:
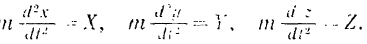
B левой части каждого из уравнении (III) содержится произведение массы точки на которую производную or одной из се координат но времени, а в правой части — проекция на соответствующую координатную ось силы, действующей на точку. Эти уравнения называются дифференциальными уравнениями движения материальной точки в декартовых координатах.
Совокупность дифференциальных уравнении движения точки выражает, очевидно, основной закон динамики точки, так же как и уравнение (106), но уже не в векторной, а в координатной, скалярной форме. Если под действием сил. лежащих в одной плоскости, точка совершает плоское движение, то оно определяется совокупностью только двух дифференциальных уравнении. Для определения же прямолинейного движения точки достаточно одного уравнения, если за координатную ось принять прямую, по которой движется точка.
Если на точку действует одновременно не одна, а несколько сил, то под проекциями 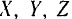 силы, действующей на точку, надо понимать, согласно закону независимости действия сил, проекции равнодействующей всех сил, приложенных к точке, равные, как известно, алгебраическим суммам проекций составляющих сил :<а соответствующие оси.
силы, действующей на точку, надо понимать, согласно закону независимости действия сил, проекции равнодействующей всех сил, приложенных к точке, равные, как известно, алгебраическим суммам проекций составляющих сил :<а соответствующие оси.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Основные законы динамики |
| Системы единиц в теоретической механике |
| Естественные уравнения движения материальной точки |
| Решение первой основной задачи динамики точки с примерами решения |
