Оглавление:
Дифференциальным уравнением 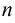 -го порядка называется уравнение вида
-го порядка называется уравнение вида 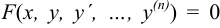 , связывающее независимую переменную
, связывающее независимую переменную 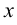 , искомую функцию
, искомую функцию 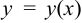 и её производные
и её производные 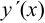 ,
, 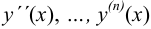 .
.
Решением или интегралом дифференциального уравнения называется любая функция 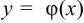 , обращающая его в тождество.
, обращающая его в тождество.
Дифференциальное уравнение первого порядка
Дифференциальным уравнением первого порядка называется уравнение вида 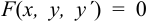 , где
, где 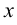 — аргумент,
— аргумент, 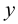 — неизвестная функция,
— неизвестная функция, 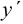 — производная от функции
— производная от функции 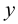 . Функция
. Функция 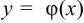 называется решением уравнения, если она обращает его в тождество, т. е.
называется решением уравнения, если она обращает его в тождество, т. е. 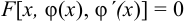 .
.
Задача Коши
Задача Коши для дифференциального уравнения первого порядка состоит в том, чтобы найти решение, которое при заданном значении аргумента 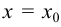 принимает заданное значение
принимает заданное значение 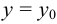 , т. е. удовлетворяет начальному условию
, т. е. удовлетворяет начальному условию 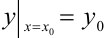 .
.
Геометрически задача Коши формулируется следующим образом: среди всех интегральных кривых данного дифференциального уравнения выделить ту, которая проходит через заданную точку 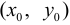 .
.
Рассмотрим несколько видов дифференциальных уравнений:
1. ДУ с разделяющимися переменными
Уравнением с разделяющимися переменными называется дифференциальное уравнение вида
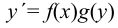
или
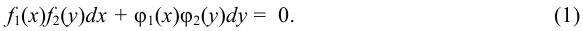
Уравнение (1) разделим на 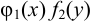 и запишем в виде
и запишем в виде
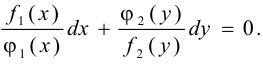
Теперь найдём общий интеграл
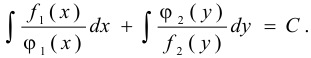
Задача №98.
Найти общее решение дифференциального уравнения
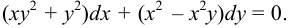
Решение:
Преобразуем левую часть уравнения
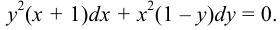
Это уравнение с разделяющимися переменными. Разделим уравнение на 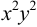 , имеем
, имеем
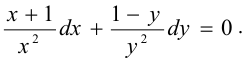
Интегрируя, получим общий интеграл уравнения
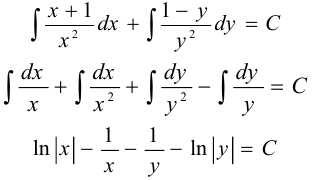
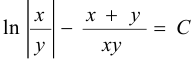 — общее решение уравнения.
— общее решение уравнения.
Задача №99.
Решить задачу Коши 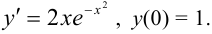
Решение:
Найдём общее решение уравнения с разделяющимися переменными:
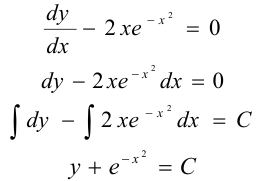
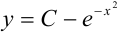 — общее решение ДУ.
— общее решение ДУ.
Решаем задачу Коши:
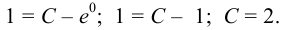
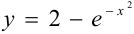 — решение задачи Коши.
— решение задачи Коши.
2. Уравнение вида
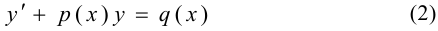
называется линейным уравнением. При этом уравнение 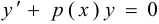 называется однородным.
называется однородным.
Общее решение линейного неоднородного дифференциального уравнения первого порядка ищется в виде 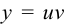 , где
, где 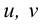 — некоторые неизвестные функции.
— некоторые неизвестные функции.
Имеем 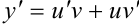 . Подставим эти замены в (2) и получим:
. Подставим эти замены в (2) и получим:
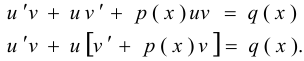
Решим теперь два уравнения:
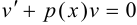 и
и 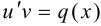 .
.
Для первого уравнения найдём частное решение с условием 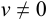 , для второго ищем общее решение. Тогда
, для второго ищем общее решение. Тогда 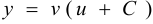 — общее решение исходного уравнения.
— общее решение исходного уравнения.
Задача №100.
Найти общее решение уравнения 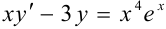 .
.
Решение:
Разделим уравнение на 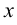 , получим
, получим
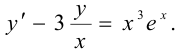
Это линейное неоднородное ДУ первого порядка.
Пусть 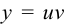 ,
, 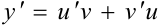 , тогда
, тогда
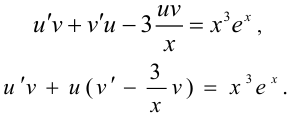
Найдём частное решение уравнения
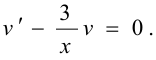
Это уравнение с разделяющимися переменными.
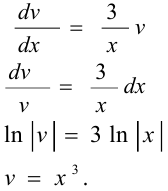
Теперь найдём общее решение ДУ
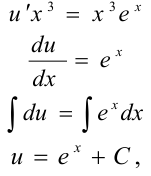
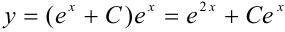 — общее решение уравнения.
— общее решение уравнения.
3. Уравнение вида 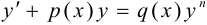 , где
, где 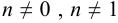 называется уравнением Бернулли. При помощи подстановки
называется уравнением Бернулли. При помощи подстановки 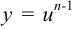 оно приводится к линейному уравнению и его можно решать подстановкой
оно приводится к линейному уравнению и его можно решать подстановкой 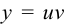 .
.
Задача №101.
Найти общее решение уравнения 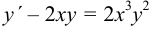 .
.
Решение:
Полагаем 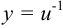 , тогда
, тогда
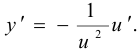
Выполняя эту подстановку, получаем линейное уравнение
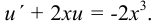
Интегрируя его, находим
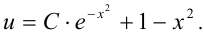
Следовательно, общее решение будет
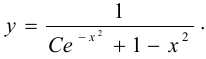
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:

