Дифференциальное уравнение изогнутой оси балки
Перемещение центра тяжести сечения по направлению перпендикулярному к оси балки Z, вызванное ее искривлением, называется прогибом балки и обозначается буквой V. В некоторых случаях в строительстве и машиностроении требуется определять прогибы. Это связано с тем, что деформации некоторых строительных конструкций лимитированы. Так, например, ограничиваются прогибы балок и плит по эстетическим соображениям или с целью уменьшить динамику конструкций. Поэтому надо уметь определять перемещения и углы поворота сечений балок. Рассмотрим консоль, испытывающую поперечный изгиб.
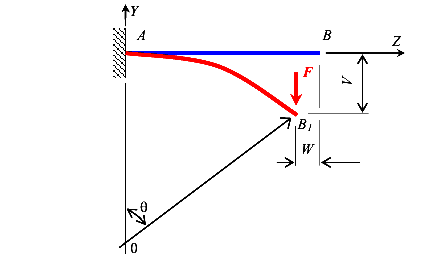
Пусть на конце консоли (рис.62) действует вертикальная сосредоточенная сила F. В результате в сечениях консоли появятся изгибающие моменты, которые приведут к искривлению балки (рис.62). Ее точка В переместится по направлению оси Z и по направлению оси Y. Эти перемещения, соответственно, обозначим W и V . Перемещение по горизонтальному направлению W незначительное и в расчетах им пренебрегают. Вертикальное перемещение (прогиб) V значительно больше горизонтального перемещения W и должно учитываться в расчетах.
Для определения прогибов воспользуемся уравнением для кривизны.

Из курса высшей математики известно, что кривизна кривой линии может быть найдена по формуле
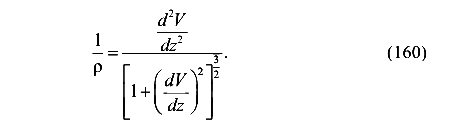
Так как для реальных балок, встречающихся в строительстве, угол поворота поперечного сечения величина малая по сравнению с единицей

то квадратом производной можно пренебречь. Тогда формула для кривизны (160) упрощается и принимает вид

Левые части уравнений (159) и (162) равны. Следовательно, равны и правые части. Тогда приближенное дифференциальное уравнение изогнутой оси балки принимает вид

Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:

