Оглавление:


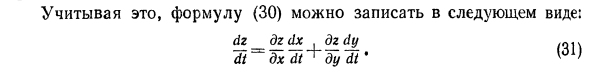






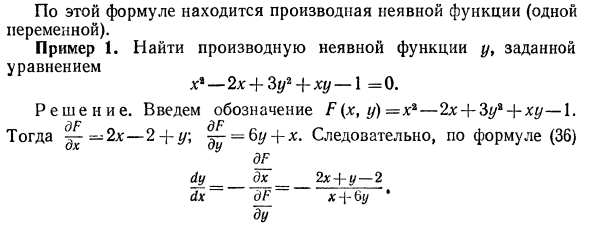

Дифференцирование сложных и неявных функций
- Отличие сложных функций от неявных функций 1. Дифференциация сложных функций Предположим, что z = f (x, y)> дано функции двух переменных, и аргумент этой функции является функцией одной независимой переменной t: x — x (t), y-. = Y (т). r — комплексная функция одной независимой переменной. Возникает проблема поиска производных Я знаю частные производные ^ и ~ для этой сложной функции ^ Производные ^ и ~. При решении этой задачи функции x = x (t) и yy (t) имеют производные в точке t, а функция двух переменных z = f (xt y) дифференцируема в соответствующей точке y) Предположим, что есть.
Условия, которым должно удовлетворять уравнение F (x, y) = 0, Чтобы определить неявную функцию у? Ответ на этот вопрос дает следующая теорема. Теорема о неявной функции. Функция F (a \ y) и ее частные производные F’x (xt y) и F’y (xt y) определены непрерывно в окрестности точки P0 (x0 \ y0) и F (xot yo) = 0, F’y (x0, yQ) Φ0, уравнение F (x, /) = 0
Не определяет функцию y (означает только фактическое значение переменной). Людмила Фирмаль
Определите уникальную неявную функцию y = y (x) и y (x0) = y0, которая непрерывно дифференцируема в интервале, включая точку x0 вблизи точки P0 (x0; y9). Эта теорема оставлена без доказательства. Пусть левая часть уравнения (35) удовлетворяет условию, указанному в теореме. Затем уравнение определяет неявную функцию y — y (x), которая содержит тождество вблизи точки p0 (* 0; y0). F (xty (x)) * что O Относительно х.
Производная функции, равная нулю, также равна нулю, поэтому полная производная дР l = 0 дх Однако согласно уравнению (32) Так где d £ _dF dF_ dy dx dx dy dx * дх ду дх ~ 1 дф DY _ DX дх дФ * (36) ду Это выражение находит производную (одну переменную) неявной функции. Пример 1. Найти производную неявной функции y, заданной уравнением 2x + 3y * + xy-1 = 0. Решения. Введено обозначение F (x, y) = x% —2x +% + xy— . дф ^ р Тогда —2x — 2 — \ — y \ = 6y — \ — x. Следовательно, формула (36) есть ди-джей dy_dx_2x + y-2 dx ~ dF_ ~ jc-i-6i / ‘du
| Частные производные | Скалярное поле |
| Полный дифференциал функции | Экстремум функций двух переменных |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Особенно в точке P2 (2; -1) ду дх , * = 2 2-f 6 (–1) 4 ‘. ‘/ = -1 Пример 2. Нахождение уравнений для касательных и кривых нормалей * xby + etv ‘- y ^ O Точка P0 (0; 1). Решения. Функция F (x, y) = x2y-f * e2v2 — Найти первую частную производную от y и значение в точке P0 (0; 1). F’x (x, y) = 2hu + y * e * yy \ F’y (x, y) к x> + 2hue * «r-1; F’A0, 1) = 1; F’y (0; 1) = -1 Используйте уравнение (36) для расчета коэффициента тангенса угла к cas ~~ dx ^ (0,1) -1 • Следующий коэффициент нормального угла / <? N = -1— = —1. Теперь найдите уравнение касательной y — 1 = 1- (g; -0) или x — y — \ — 1 = y0, и нормальные уравнения y- \ = -1 (x-0) или x + y-1 = 0. 2-2—1—2 1
Присвойте приращение D / независимой переменной t. Функция z дифференцируема по предположению, поэтому ее полный прирост Δ можно выразить в виде Ar = g Ax + 1 Du + o (Ax, D * /), (29) далее 11sh — 0, где p = KDx2 + D ^ / a. p-> o P Разделив обе части равенства (29) на Dt и передав их до предела как At -► 0, получим: n £ * lim% + Hin lim * (30) d / ^ 0D / OX A / oD ‘dU A / -o L / D / — * 0L’
Переменные x и y получают приращения Ax и Du соответственно, а функция r получает приращение Ar. Людмила Фирмаль
Если каждый предел существует в правой части этого уравнения, то есть предел в левой части Производная этого уравнения, т. Е. Дифференциал Но ~ lim ~ = и limτm = r dt d / -, oA ‘dt d / -> oL / dt Существует по предположению. Найду Lim Lim F-. ^ W Hm®. ободок Д / ОД / -. 0ХРЛ / / А / — »0 ПД / ^ 0Д / Рассмотрим сначала Ита лим-д / -> о д / — »» об А / Производные ~ и dt At- * o P как At-> 0, прежде чем найти предел И р—> 0 **. Но тогда liin- = lim- = 0, так д / -оРр-> оР
Учитывая это, уравнение (30) можно записать в следующем формате: dz_dzdx. dzdy Jt ~ d ~ x ~ di’d ~ yTf Пример 1. Найти производную ^, если 2 = xy, x = sint, y = tz. Решения. (} Применение Jurmula (31) Tt = W *% + WYvjt ~ yxy-1 (s \ nt) ‘+ xy \ nx (/ «)» = -yxy ~ l cos * + xY В x. 2t = t2 (sin «: 1 COS t -f -2 / (грех /) <J в грехе t = = t (грех (‘cos t + 2 sin t • в грехе t). Теперь рассмотрим функцию r = f (x, //) при условии y-y (x). Где переменная r является функцией одной переменной x. z— = f (jc, r / (jc)). Этот случай сводится к предыдущему, и роль переменной t играет x. Из уравнения (31) dz_dz dx, dg dy dx ~~ dx ‘dx ~ i ~ dy’ dx ‘ Но ^ -1, так dz dg.dg dy, 0o \ Tx-Fx ^ Ty’Tx ‘
Правая и левая части этого уравнения содержат производную от r по x. Одна из них является частной производной функции двух переменных * = f (*, y). Это может быть найдено, как будто у не зависит от х. В отличие от производных слева Часть уравнения (32) является производной комплексной функции одной переменной z = * f (x, y, (*)). Эта производная называется совершенной производной. Предположим, что z = f (x, y). Где x = x (u, v) и y (u, v). В этом случае z является комплексной функцией двух независимых переменных u и y. Найти частную производную этой комплексной функции dz dz ЦИИ * Г и Я- Я т дг дх ди * Частные производные и-найдены так, как если бы z, x, y были функциями одной переменной и. Но вы можете
Используя уравнение (31), производные ^, ~ и ^ Соответствующие частные производные: ~, ~ и дг _ дг дх дг ду Точно так же вы можете получить следующее выражение dg __dg dx dg doo Полученный результат легко обобщается для комплексных функций с любым конечным числом аргументов.
В частности, для функции трех переменных u = F (x, //, r), g.-e x = x (t) t y = y (t), z = z (t) du___dF_ dx.dF dy, dF_dz от dt до dx ‘dt dy * от dt до r до dg’ dt ‘ Пример 2. Функция z arctg-, где x- и в y = x iir-Vy удовлетворяет следующему соотношению: дг. <] r u-y dv dv ~ v2 — \ — u2 ‘ Решения. Поиск — £ y f X_Y 1_ x Y} x, ■ V y) y. 1 год u2 гм. X2 ‘y’ ^ 1 y2 I and> » 14— 1 + -1 год 8 ■ — £ ■■ 1 + 1 • f)> + * + — 1 х От X2 до ‘X2-я- * Y2 Теперь у нас есть 4- = 4-й + * да ‘да + х2 + т / 2 2 года Xg + y- Если вам нужно доказать. 2 (а-а) 2 (а-во) _ и-а
Инвариантность формы полной дифференциации Как известно, форма инвариантна для производной функции от одной переменной y / (x). Это потому, что дифференциальное уравнение dy = f ‘(x) dx Это остается верным независимо от того, является ли x независимой переменной или функцией переменной: x = μ (t) (см. Главу VI, § 3, пункт 4). Для функции с несколькими переменными u = f (x, y, r, …, f) выполняется аналогичное утверждение: n переменных uf (xt y, r, …, f) Полная производная функции сохраняет свою форму , Di. Ди ди, ди
l Независимо от того, являются ли *, y, z, …, t независимыми переменными или функциями других переменных. Ограничение доказательства этого утверждения только для функций с двумя переменными z = f (x, y). Как вы знаете, если x и y являются независимыми переменными, общая разница имеет вид dz = tdx +% dy- Указывает, что эта форма производной сохраняется, когда x и y становятся функциями новых переменных: u), y-y (u, u). В этом случае z является комплексной функцией от u и u.
Производная этой сложной функции дается dz = p-du +% dv. Ди 1 ди Однако согласно уравнениям (33) и (34) дг _ дг_ дх, дз до ди дх ди до * ди9 dg _ dg_ dh .dz do ди дх ди ‘до ди’ так , (Dz dx, dg dy . (Dg dx, dg dy \, dz = (Tx-Tu + ry-fu) du + (Tx-d-o + d-y-i) dv = j * d0 + *. ftdu + *. д’и .. дх ди 1 дх ди дю ди дю ду — £ (£ * + £ *) + t (a> + t>) = с того времени дг. DZ = didx + jydy> * ~ Du + ^ dv = dx, a ^ du — \ — ^ dv = dy Поэтому вся минута дз не меняет своей формы. дз, дз ты Когда x и y являются функциями других переменных
Неявное разграничение функций Как вы знаете, неявная функция аргумента x дается F (x, y) = 0, (35) Не допускается для y (см. Главу VI, § 1, стр. 15) Я знаю, что не все уравнения, связывающие x и y, определяют неявные функции. Например, уравнение х * + у2 + 1 = 0

