Оглавление:




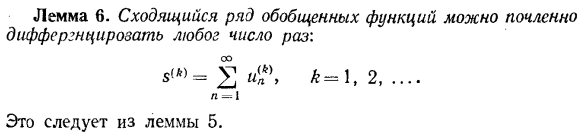

Дифференцирование обобщенных функций
Дифференцирование обобщенных функций. Здесь мы определяем производную обобщенной функции. Во-первых, давайте уточним, что такое непрерывная дифференцируемая производная по нормальной функции / числовой оси, которая считается функционалом на O ( / ’ , φ).Особенности. * Ю. В., Сохоцкий (1842-1929) русский математик. 59.4.Дифференцирование функций обобщения 527. Из-за конечности функции при интегрировании с каждой частью верно следующее: + 00 4-ОО (Г. Φ)= ^ р(х) Φ (х) Φ (х) ух = $ / () ψ(х)ух =([, па), (59.17) Оо-оо. И, как вы знаете, f’ey. So, производная/ ’является функционалом B, и ее значение выражается значением функции/, которая считается функционалом, используя выражение (59.17).Это делает естественным следующее определение.
Операция вычисления производной обобщенной функции называется, как и в случае нормальной функции, дифференциальной. Людмила Фирмаль
- Определение 20.Производная обобщенной функции/называется функционалом на B, обозначается через/ и определяется уравнением. ( / ’ .φ)= (Aφ’) Φ0. (59.18) Другими словами, значение функционала в любой точке p в пространстве 0 / равно значению функционала в обратном знаке P’e B/. Итак, обобщенная функция имеет вид derivative. In смысл определения 20, есть производные функций, которые могут быть локально интегрированы! Из уравнения (59.17) видно, что дифференцирование в обычном смысле непрерывно дифференцируемой функции по числовой оси, рассматриваемой как функционал на B, совпадает с дифференцированием в смысле обобщенной функции.
Лемма 4.Функция/является линейной непрерывной функцией и, следовательно, обобщенной функцией. Доказательство. Проверьте линейность. (Γ, РП + ПФ)= (/.(РП + ПФ)’) =(/, РП + ПФ)) = (( / , FO-MAΦ ’) =Я (/’, Φ)+ ((/\Φ), Φ^ ^О. Для проверки непрерывности функции/Φ0, φ e A = 1, 2,…Если, и тΦ* = = φ 0、 к * ОО По определению сходимости в пространстве B、 к* * * ОО В B; следовательно, в случае Φ-Φ Б, Пη (/ ’, φ)=-тη (/, ϕ&)= к * СО к * СО = ( / , Φ’) =(G. Φ). Поэтому, если (ее’, то /’всегда присутствует, и[’Е ее’ если Производные более высокого порядка обобщенной функции определяются последовательно, как и обычные функции. / » = ( / ’)’./ ’» = ( / «) ’ Пятьдесят два В общем § 59.Обобщенная функция p) = phy-1) Y 6 = 1, 2,…,/»=/. С помощью индукции вы можете легко проверить следующее 6 = 0, 1,… (/’ * , Ф)= ( ~ !) *(ЛФеО.
- Согласно этому определению, обобщенная функция имеет производную любой степени. Или, как мы иногда говорим, бесконечно дифференцируемы. Пример 1.Пусть будет так { 1, если x> 0, Если 0, если x0. 0 (х)= Функция 0 (x) называется функцией Хевисайда (см. (59.10)) или блоком function. It можно считать обобщенной функцией, поскольку она может быть интегрирована локально. Найдите его производные. Согласно определению(59.18)、 + ОО-4-ОО (0′, φ)=-(0, φ’)= ^ 6 (x) φ ’( * ) yx = $φ’(x)yxО, да. =φ (0)=(b, φ), фе9、 То есть, 0 ’= 6 (n. по сравнению с 59.1). 2.As другой пример, вычислить производную от функции 8 (6*, Ф)=( -!) *(B, Ф (*)) =(-1) * ф () (0). Практические вопросы 10. / И G к обобщенной функции и и и-к графу. Доказать это (Я / + э) ’ = я /’ + РД’. / г. 12.
Доказать это Один \ \ 9 (x) 81OXOX _, = 8 (x). для / Х | 13. 6р (х)= |если O для / x | Восемь 2 ’ Затем, в пространстве обобщения 11.Γ^ -) ^ ^ 9 (x)= докажите, что это b (x). Особенности 11т быть (х)= B (X; и 8е (х)= 8-0 (M) x x»дело、 14. пусть f (x)= ’ функция (x) и} 2 (x) непрерывны I x 1 x(x)», Лига Чемпионов«. Дифференцируемо и дифференцируемо, есть предел/(x0, 0).Найти производную} ’(x) в пространстве O’. 15.Сделайте функцию / (x) непрерывно дифференцируемой по числовой оси. Найти производную (9/) «в пространстве». 59.4.Дифференцирование функций обобщения 529. 16.Докажите, что в пространстве O выполняется следующее уравнение:?5 =(1n / x]) «(см. Упражнение 5). 17. Докажите, что вы равны 4-ОО ^ Ш $ * = Г + я ^ ^(ДС-2кп. Н = 1 к = ОО Используйте формулу индикации(см. Пример 55.4, раздел 3) 81P рН д. О 2L Н-1 Лемма 5. Пусть /» ее», / ЭО’и И затем… 11GT1/; г (59.19) (59.20 )) гл.
Для последовательности обобщенных функций, сходящихся в D’, производная предельной функции равна пределу производной последовательности. Людмила Фирмаль
- Доказательство. Для всех функций Фео ( / ’ .( / ) = [( / .Ф’) ( / «, ф’)] * 0 как n + oo、 Ф борьбы. Да. Вы также можете рассмотреть набор обобщенных функций ОО Е (59.21) Один Где^ n \ n \ n-1, 2, всего н $ н-н * 4 = 1 Является n-порядком ряда (59.21) (n = 1, 2,…называется частичной суммой. Если существует ограничение на O1, то ряд (59.21) называется сходимостью 1]Щ5Я= I p-объектно-ориентированный Обобщенная функция x называется суммой ряда (59.21). она записана. ОО 5-Ул Ун. n-1§ 59.Обобщенная функция Пятьсот тридцать Лемма 6.Набор функций сходимости может быть дифференцирован столько раз, сколько один член. И н = И.
Смотрите также:
Решение задач по математическому анализу

