Оглавление:



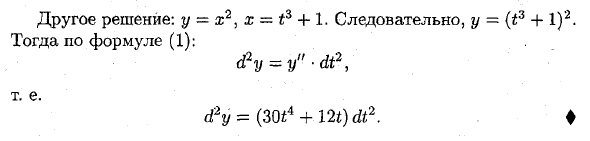
Дифференциалы высших порядков
- Разница более высокого порядка Пусть y = f (x) — дифференцируемая функция, а ее аргумент x — независимая переменная. И его первая производная dy = f ‘(x) dx также является функцией x, вы можете найти производную этой функции. Производная от производной функции y = f (x) называется второй производной (или второй производной) и выражается как d2y или d2f (x). Следовательно, по определению cPy = d (dy).
Поскольку dx = J не зависит от x, постоянная dx учитывается при дифференцировании. d2y = d (dy) = d {f ‘(x) dx) = {f’ (x) dx) » dx = / «(a?) dx-dx = f» {x) (dz) 2t. е. d2y = f «(x) dx2 (1) Где dx2 — это (dx) 2. Третья производная определяется и определяется таким же образом. d3y = d (d2y) = d (f «(x) dx2) = f ‘(x) (dx) \ И вообще, n-я производная является производной (n-1) -производной: dny = d (dn ~ ly) = / M (®) (sv) l. Отсюда видно, что f ^ n \ x) = ^ jjh, особенно когда n = 1, 2, 3 и так далее. «■> -r-> • <*> — & ■ um.
Найти выражение для второй производной функции y = f (x). Людмила Фирмаль
Другими словами, производная функции может рассматриваться как отношение между производной соответствующего порядка и степенью дифференциации соответствующей независимой переменной. Обратите внимание, что все вышеприведенные выражения действительны, только если x является независимой переменной.
Для функции y = f (x), где x — функция других независимых переменных, формальное свойство инварианта для производных второго или более высокого порядка отсутствует, и оно вычисляется с использованием других выражений. Это показано на примере второй производной.
| Основные теоремы о дифференциалах. Таблица дифференциалов | Теорема Ролля |
| Применение дифференциала к приближенным вычислениям | Теорема Коши |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Используя формулу дифференциала произведения (d (u • v) »-v dun- и dv): d2y = d (f ‘(x) dx) = d (f’ (x)) dx + f ‘(x) • rf (dar) = / «(*) dx + /’ (x) • d * ®, Это d2y = f «(x) dx2 + -f ‘(x) -d2x. (2) Сравнивая уравнения (1) и (2), мы видим, что вторая производная изменяется в случае комплексных функций. Второй член f ‘(x) -d2x отображается. Если х является независимой переменной, d2x = d (dx) = d (1 • dx) = dx • d {1) = dx-0 = 0 И уравнение (2) входит в уравнение (1).
Пример: 1) Если y = e3zh и x — независимая переменная, найдите d2y. ♦ y ‘= 3e3 *, y «= 9e3z, поэтому уравнение (1) имеет cPu = 9e3x dx2 4 2) Если y = x2 и x = f3 + 1, а t является независимой переменной, найдите d2y. ♦ Используйте формулу (2). y ‘= 2x, y’ = 2, dx = 3 £ 2 dt, d2x = 6f A2, тогда = 2dx2 + 2x-6t dt2 = 2 (3 £ 2 dt) 2 + 2 (£ 3 + 1) 6 * eft2 = = 18t4 <it2 + 12t4 dt2 + 12i dt2 = (30t4 + 120 dt2.Другое решение: у = х2, х = £ 3 + 1. Следовательно, y = (t3 + 1) 2.
Тогда согласно уравнению (1):Людмила Фирмаль

